Search for neutrinoinduced cascades with the AMANDA detector

J. Ahrens,

X. Bai,

G. Barouch,

S. W. Barwick,

R. C. Bay,

T. Becka,

K.H. Becker,

D. Bertrand,

F. Binon,

A. Biron,

S. Bo

ser,

J. Booth,

O. Botner,

A. Bouchta,

O. Bouhali,

M. M. Boyce,

T. Burgess,

S. Carius,

A. Chen,

D. Chirkin,

J. Conrad,

J. Cooley,

C. G. S. Costa,

D. F. Cowen,

A. Davour,

C. De Clercq,

T. DeYoung,

3,†

P. Desiati,

J.P. Dewulf,

P. Doksus,

P. Ekstro

T. Feser,

J.M. Fre

re,

T. K. Gaisser,

M. Gaug,

H. Geenen,

A. Goldschmidt,

A. Hallgren,

F. Halzen,

K. Hanson,

R. Hardtke,

T. Hauschildt,

M. Hellwig,

G. C. Hill,

P. O. Hulth,

K. Hultqvist,

S. Hundertmark,

J. Jacobsen,

A. Karle,

J. Kim,

B. Koci,

L. Ko

pke,

M. Kowalski,

J. I. Lamoureux,

H. Leich,

M. Leuthold,

P. Lindahl,

I. Liubarsky,

D. M. Lowder,

5,‡

J. Madsen,

P. Marciniewski,

H. S. Matis,

C. P. McParland,

T. Messarius,

T. C. Miller,

2,§

Y. Minaeva,

P. Mioc

inovic

P. C. Mock,

R. Morse,

T. Neunho

ffer,

P. Niessen,

D. R. Nygren,

H. Ogelman,

Ph. Olbrechts,

C. Pe

rez de los Heros,

A. C. Pohl,

R. Porrata,

4,¶

P. B. Price,

G. T. Przybylski,

K. Rawlins,

C. Reed,

E. Resconi,

W. Rhode,

M. Ribordy,

S. Richter,

J. Rodrı

guez Martino,

P. Romenesko,

D. Ross,

H.G. Sander,

K. Schinarakis,

T. Schmidt,

D. Schneider,

R. Schwarz,

A. Silvestri,

M. Solarz,

G. M. Spiczak,

C. Spiering,

N. Starinsky,

3,††

D. Steele,

P. Steffen,

R. G. Stokstad,

K.H. Sulanke,

I. Taboada,

16,‡‡

L. Thollander,

S. Tilav,

M. Vander Donckt,

W. Wagner,

C. Walck,

C. Weinheimer,

C. H. Wiebusch,

C. Widemann,

R. Wischnewski,

H. Wissing,

K. Woschnagg,

W. Wu,

G. Yodh,

and S. Young

AMANDA Collaboration

Institute of Physics, University of Mainz, Staudinger Weg 7, D55099 Mainz, Germany

Bartol Research Institute, University of Delaware, Newark, Delaware 19716

Department of Physics, University of Wisconsin, Madison, Wisconsin 53706

Department of Physics and Astronomy, University of California, Irvine, California 92697

Department of Physics, University of California, Berkeley, California 94720

Fachbereich 8 Physik, BUGH Wuppertal, D42097 Wuppertal, Germany

Universite

Libre de Bruxelles, Science Faculty CP230, Boulevard du Triomphe, B1050 Brussels, Belgium

DESYZeuthen, D15735 Zeuthen, Germany

Division of High Energy Physics, Uppsala University, S75121 Uppsala, Sweden

Department of Physics, Stockholm University, SCFAB, SE10691 Stockholm, Sweden

Department of Technology, Kalmar University, S39182 Kalmar, Sweden

Department of Physics, Pennsylvania State University, University Park, Pennsylvania 16802

Vrije Universiteit Brussel, Dienst ELEM, B1050 Brussel, Belgium

Lawrence Berkeley National Laboratory, Berkeley, California 94720

Physics Department, University of Wisconsin, River Falls, Wisconsin 54022

Department of Physics and Astronomy, University of Pennsylvania, Philadelphia, Pennsylvania 19104

Received 27 June 2002; published 10 January 2003

We report on a search for electromagnetic and/or hadronic showers

cascades

induced by a diffuse flux of

neutrinos with energies between 5 TeV and 300 TeV from extraterrestrial sources. Cascades may be produced

by matter interactions of all flavors of neutrinos, and contained cascades have better energy resolution and

afford better background rejection than throughgoing

induced muons. Data taken in 1997 with the

AMANDA detector were searched for events with a highenergy cascadelike signature. The observed events

are consistent with expected backgrounds from atmospheric neutrinos and catastrophic energy losses from

atmospheric muons. Effective volumes for all flavors of neutrinos, which allow the calculation of limits for any

Present address: CERN, CH1211, Gene

ve 23, Switzerland.

†

Present address: Santa Cruz Institute for Particle Physics, University of California, Santa Cruz, CA 95064.

‡

Present address: MontaVista Software, 1237 E. Arques Ave., Sunnyvale, CA 94085.

Present address: Johns Hopkins University, Applied Physics Laboratory, Laurel, MD 20723.

Present address: Optical Networks Research, JDS Uniphase, 100 Willowbrook Rd., Freehold, NJ 077282879.

Present address: L174, Lawrence Livermore National Laboratory, 7000 East Ave., Livermore, CA 94550.

Present address: Dept. of Physics, Massachussetts Institute of Technology, Cambridge, MA 02139.

††

Present address: SNO Institute, Lively, ON, Canada P3Y 1M3.

‡‡

Present address: Dept. de Fı

sica, Universidad Simo

n Bolı

var, Apdo. Postal 89000, Caracas, Venezuela.

PHYSICAL REVIEW D

, 012003

2003

05562821/2003/67

/012003

0120031

neutrino flux model, are presented. The limit on cascades from a diffuse flux of

(

)

9.8

GeV cm

, assuming a neutrino flavor flux ratio of 1:1:1 at the detector.

The limit on cascades from a diffuse flux of

(

)

6.5

GeV cm

, indepen

dent of the assumed neutrino flavor flux ratio.

DOI: 10.1103/PhysRevD.67.012003 PACS number

: 14.60.Lm, 95.55.Vj, 95.85.Ry, 96.40.Tv

I. INTRODUCTION

Neutrinos interact principally via the weak force, posing a

detection challenge for neutrino telescopes but bestowing a

valuable advantage on the field of neutrino astronomy: neu

trino fluxes from astronomical sources are essentially unat

tenuated even over cosmological distances. In contrast, high

energy gamma rays are absorbed and/or scattered by

intervening matter and photons, and highenergy cosmicrays

are deflected by galactic and intergalactic magnetic fields

except at the highest energies (

eV).

We present a search for the fully reconstructed light pat

terns created by electromagnetic or hadronic showers

cas

cades

resulting from a diffuse flux of highenergy extrater

restrial neutrinos. We use data collected in 1997 from the

Antarctic Muon and Neutrino Detector Array

AMANDA

for this purpose. Demonstrating

induced cascade sensitiv

ity is an important step for neutrino astronomy because the

cascade channel probes all neutrino flavors, whereas the

muon channel is primarily sensitive to charged current

and

interactions. This is particularly relevant in view of

the emerging understanding of neutrino oscillations

1–4

,in

which the flux of

would be reduced by oscillations.

The

detection of highenergy atmospheric muon neutrinos by

AMANDA has been demonstrated by the full reconstruction

of Cherenkov light patterns produced by upgoing muons

5–7

Cascades also boast more accurate energy measure

ment and better separation from background, although they

suffer from worse angular resolution and reduced effective

volume relative to muons. Importantly, it is straightforward

to calibrate the cascade response of neutrino telescopes such

as AMANDA at lower energies through use of, e.g.,

in situ

light sources. Furthermore, cascades become increasingly

easier to identify and reconstruct as detector volumes get

larger, so the techniques presented here have relevance for

future analyses performed at larger detectors.

Electron neutrinos can produce cascades with no detect

able track via the charged current

interaction and all

neutrino flavors can produce cascades via the neutral current

interaction. Cascadelike events are also produced in

CC interactions when the resulting

decays into an electron

roughly 18% branching ratio

or into mesons

roughly 64%

branching ratio

and the

energy is below about 100 TeV, at

which energy the

decay length is less than 5 m, so that the

shower produced by the neutrino interaction and the shower

produced by the

decay cannot be spatially resolved by

AMANDA. The contribution of

to the cascade channel

becomes important when flavor oscillations are taken into

account for extraterrestrial

8–10

and for atmospheric

induced cascades. For extraterrestrial sources, current

knowledge of neutrino oscillations suggests a detected neu

trino flavor flux ratio of

::1:1:1 following an ex

pected flux ratio of 1:2:0 at the source.

The total light output of an electromagnetic cascade is

approximately 10

photons/TeV in ice. Hadronic cascades

have a light yield about 20% lower

. An electromagnetic

cascade develops in a cylinder of about 10–15 cm in radius

Molie

re radius

and several meters in length

about 8.5 m

from the vertex of a 100 TeV cascade, essentially all charged

particles are below the critical energy

. Hadronic cascades

have longer longitudinal developments and larger Molie

radii. As a sparsely instrumented detector, AMANDA is in

sensitive to the topological differences between electromag

netic and hadronic cascades. Since the NC interaction has a

lower cross section and results in a deposition of less energy

than the CC interaction, and since we assume a steeply fall

ing neutrino energy spectrum, at any given energy a very

small fraction of the

events are due to NC interactions.

Hence their impact on the cascade energy resolution is small,

and the energy spectrum of reconstructed cascades closely

follows that of the CC

energy spectrum.

In this paper, we present limits on the diffuse fluxes of

(

) and (

), assuming a cus

tomary

power law spectrum at the source. These limits

are based on the observation of no events consistent with a

diffuse flux of highenergy extraterrestrial neutrinos. We also

present effective volumes for all neutrino flavors to facilitate

the calculation of a limit for any flux model.

A search for

upgoing muons produced by a

extraterrestrial diffuse

flux is presently being conducted and preliminary results

have been reported in

II. THE AMANDAB10 DETECTOR

The data used in this work were taken with the

AMANDAB10 detector in 1997. AMANDAB10

6,7,14

was commissioned in 1997 with a total of 302 optical mod

ules

OMs

arranged on 10 strings, at depths between 1500

m and 2000 m below the surface of the ice at the South Pole.

The strings are arranged in two concentric circles 35 m and

60 m in radius, with one string at the center. The OMs in the

inner four

outer six

strings have a 20 m

10 m

vertical

separation. Each OM contains a 20 cm photomultiplier tube

PMT

in a spherical pressure vessel. Coaxial cables in the

inner four strings and twisted pair cables in the outer six

strings provide high voltage to the PMTs and simultaneously

transmit their signals to the electronics housed on the sur

face. The detector is triggered using a majority condition in

which an event is recorded if more than 16 modules have a

signal

i.e., were ‘‘hit’’

ina2

s time window. A total of

1.05

events were recorded during an effective live time

of 130.1 days.

J. AHRENS

et al.

PHYSICAL REVIEW D

, 012003

2003

0120032

The optical properties of the ice have been studied with

situ

light sources and with atmospheric muons. These studies

have shown that ice at the South Pole is not perfectly homo

geneous, but rather consists of horizontal layers correspond

ing to global climatological conditions in the past, such as

ice ages. These layers lead to a modulation of the absorption

and effective scattering lengths as a function of depth

Optical properties are also modified by the presence of drill

hole bubbles which are created during the drilling and de

ployment processes.

III. METHODS FOR CASCADE RECONSTRUCTION

Simple reconstruction algorithms are initially applied to

the data. These methods are used to reduce the data sample

size and to seed more sophisticated reconstruction algo

rithms, while maintaining high passing rates for simulated

signal events. For cascades, the mean position of the hit

OMs, or

center of gravity

, is used as the first guess of the

position. In order to efficiently reject muons, they too are

reconstructed, beginning with a first guess track fit called the

line fit

. The line fit is an algorithm that assumes that hits

can be projected onto a line, and that the particle which

produced the hits travels with a velocity

line

and has a start

ing point

. The fit minimizes the quantity

(

hits

(

line

)

as a function of

and

line

, where N

hits

is the

number of hits in the event. These procedures are described

in more detail elsewhere

17,18

After calculating the first guesses, three maximum likeli

hood methods are used consecutively to reconstruct precisely

the cascade vertex position, time, energy and direction.

These methods are described below.

A. Single photoelectron vertex position and time reconstruction

The cascade vertex position and creation time are recon

structed using a maximum likelihood function that takes into

account the Cherenkov emission, absorption and scattering

of light. This vertex information is required for rejecting po

tential backgrounds and for subsequent fits for energy and

direction. This procedure is quite similar to the algorithms

used for muon fitting

. A more comprehensive descrip

tion of the different cascade reconstruction methods can be

found in

18–20

We use a likelihood function having the form

spe

)

hits

res

where

res

hit

Cher

is the difference between observed hit

time and expected time for Cherenkov emission without

scattering—the

time residual

—and

(

res

) is the probabil

ity of observing a photon at a time residual

res

at a distance

from the emitter. The label ‘‘spe’’ indicates that

spe

sumes all hits are due to single photoelectrons.

The probability

(

res

) was generated by parametrizing

simulations of light propagation in ice. The product in Eq.

is calculated using all hit OMs. The maximization of

spe

provides a significant improvement over the center of gravity

in the estimation of the vertex position and time of the cas

cade. The estimate will be further improved by the multi

photoelectron reconstruction descrived below.

B. Multiphotoelectron vertex position and time reconstruction

The single photoelectron likelihood can be refined by tak

ing into account that the time measured in each PMT is the

time of the first photon to be observed. If a PMT receives

photons, the probability of measuring a time residual,

res

and the associated likelihood function are

res

‘

mpe

)

hits

res

where the ‘‘mpe’’ label indicates that

mpe

describes multi

photoelectron hits. In AMANDA we use the measured pulse

amplitude as an estimator for

The maximization of

mpe

is used to estimate the most

likely vertex position

and time

of a cascade. The multi

photoelectron vertex reconstruction uses the maximization of

spe

to seed initial values of cascade vertex position and

time.

C. Energy and direction reconstruction

Cascade energy and direction are reconstructed using a

likelihood function assembled from the probabilities of an

OM being hit or remaining unhit assuming a cascade hypoth

esis:

)

Hit OMs

Hit

)

Unhit OMs

Unhit

Maximization of

provides the most likely value of en

ergy

and direction

of a cascade. Note that in principle

this procedure also allows for the reconstruction of position

but not time

of a cascade. Monte Carlo studies have shown,

however, that the position resolution obtained by maximizing

is not as good as that obtained with

spe

mpe

IV. DETECTOR RESPONSE TO CASCADES

In the absence of a tagged source of highenergy neutrino

induced cascades, to understand the response of the detector

we rely on

in situ

light sources, catastrophic energy losses by

downgoing cosmicray muons, and Monte Carlo simula

tions. The successful reconstruction of these data demon

strate detector sensitivity to cascade signals.

A. Pulsed laser

A pulsed laser operating at 532 nm on the surface is used

to send light through optical fibers to diffuser balls embed

ded in the ice close to almost every OM in the detector. A

comparison of Monte Carlo and experimental data for these

SEARCH FOR NEUTRINOINDUCED CASCADES WITH . . . PHYSICAL REVIEW D

, 012003

2003

0120033

in situ

light sources deepens our understanding of recon

struction performance and detector signal sensitivity. The

photon intensity that can be produced at each diffuser ball is

not known

a priori

, so we force the number of hit channels

in experimental and simulated pulsed laser data to match.

Thus, the simulations predict that the laser produces pulses

in the ice comprising 5

photons

correspond

ing to a maximum cascade energy of roughly 10 TeV

. The

laser pulses are roughly 10 ns wide, short enough to mimic

the time structure of true cascades.

Although highly useful as a cascade calibration source,

the pulsed laser system has some minor drawbacks. The dif

fuser ball light output is expected to be isotropic, so the laser

data does not provide information about the angular response

of the detector to cascades. The laser produces light at

532 nm and at this wavelength the optical ice properties

are different from those at Cherenkov radiation wavelengths.

The effective scattering length at 532 nm is 18–30 m and

depends on depth. The absorption length at 532 nm is 25 m

and independent of depth

at the shorter wavelengths

characteristic of Cherenkov radiation the absorption length is

about 100 m

Independent data sets taken with diffuser balls in a variety

of locations are reconstructed with the first guesses and with

the timeposition reconstruction algorithm described above.

The position resolution is about 1 m in the

dimension and

about 2 m the in

and

. It is better in

due to closer OM

spacing in that dimension.

The pulsed laser simulation uses a simplified optical

model of ice properties: the drillhole bubbles are taken into

account, but no depth dependence is used for the scattering

length. In spite of this simplification, the vertex resolution of

the pulsed laser data agrees well with simulations, showing

that the detector can be used to reconstruct the position of

contained pointlike events.

Contained events are defined as

events whose reconstructed vertex lies within a right cylinder

of height 400 m and radius 60 m, centered on the

AMANDAB10 detector and encapsulated by it.

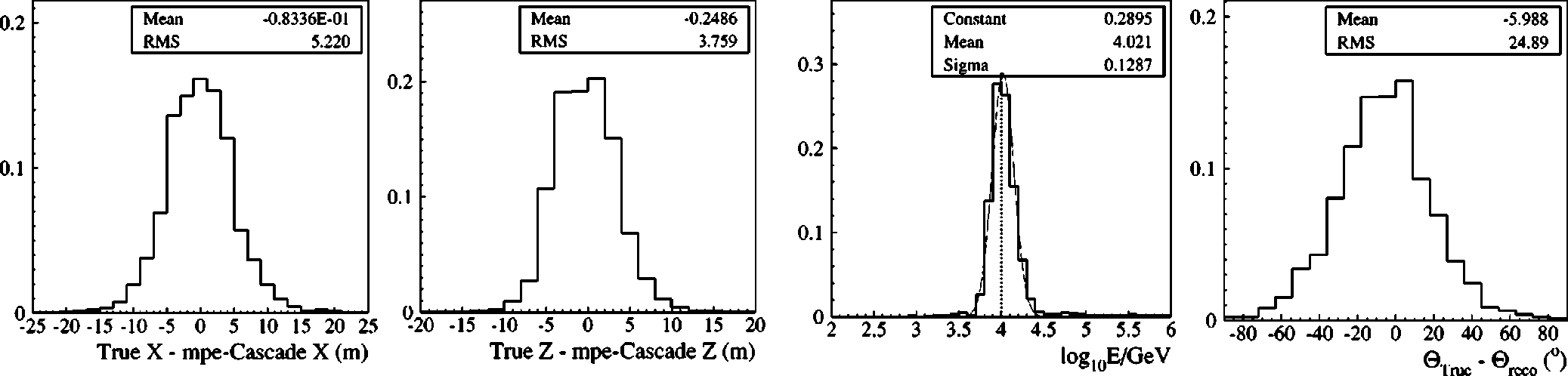
Figure 1

FIG. 1. The figure shows four plots with results of the reconstruction of pulsed laser data

solid

and simulation

dashed

with the diffuser

ball next to OM 69

situated near the center of the detector

. The differences between simulated and reconstructed

and

components of the

position, the speed of the line fit,

line

, and the reduced likelihood parameter,

mpe

, are shown. The vertical scale for all four plots is

arbitrary. The position of the OM is known with about 1 m precision

, so there is no discrepancy in the reconstructed

plot. The

discrepancy in the likelihood parameter plot arises due to the simplified ice model used for the pulsed laser.

TABLE I. Selection criteria used in the search for highenergy

induced cascades with AMANDAB10.

The number of events left after applying each selection criterion to experimental data and background

simulations of atmospheric

and

are shown. We simulated 20.3 days of atmospheric

data, and

130.1 days of atmospheric

and

. Signal simulation is also shown for

and

assuming

spectra, a flux of 1

GeV

Selection criteria Expt. data Atm

Atm

Trigger 1.05

1.51

369.9 245.5 12446 12150

big TOT

line

0.12 or

hits

0.35

dir

spe

8or

hits

spe

7.4 or

hits

5.57

1.12

51.1 40.4 2727 3424

mpe

7.1

1.50

2.03

38.2 30.7 2128 2818

dir

mpe

1.26

1.14

32.1 26.2 1909 2520

80° 3.62

2.47

22.5 18.5 1105 1676

9 Slices in

1.48

1.19

10.6 8.5 528 711

10 cos(

)

0.6 675 84 1.3 1.0 106 156

mpe

0 0 0.01 0.01 28.7 43

J. AHRENS

et al.

PHYSICAL REVIEW D

, 012003

2003

0120034

shows the results of the reconstruction of pulsed laser data

and simulation.

B. Catastrophic muon energy losses

The vast majority of the events recorded by AMANDA

are downgoing muons induced by cosmicray air showers.

This background has been simulated with the

CORSIKA pro

gram

using the average winter air density profile at the

South Pole and the

QGSJET hadronic model

option. The

cosmicray composition is taken from

. The propagation

of muons through ice is simulated with the program

MUDEDX

25,26

. Optical properties of the ice, including depth depen

dence and drillhole bubbles, are also simulated.

From the large sample of atmospheric muons it is possible

to extract a subset of cascadelike events in which the ma

jority of the recorded hits come from catastrophic, localized

energy loss of the muon

e.g., a bright bremsstrahlung

. The

extraction of these events is achieved using criteria 1–9 from

Table I, i.e., we do not require these events to reconstruct as

upgoing cascades.

We do, however, still reject obvious

downgoing muons via criterion number 8.

Based on the

number of hits produced by the brightest cascade in simu

lated events, and on a visual study of these events, we have

confirmed that after applying these selection criteria the re

maining events are indeed cascadelike.

Figure 2 shows the energy spectra of muon energy losses

for experimental data and simulated atmospheric muons. The

experimental and simulated data agree reasonably well, but

not perfectly. The difference is discussed in Sec. VI.

C. Monte Carlo prediction for neutrinoinduced

cascade reconstruction

To study the performance of the reconstruction algorithms

we simulated a flux of

following an

power law

spectrum. Neutrinos from astrophysical sources are expected

to have a hard spectrum, reflecting the processes in the cos

mic accelerators that generate them. Earth absorption and

NC scattering are taken into account in the simulation. The

‘‘preliminary reference Earth model’’ is used to calculate the

Earth’s density profile

. We calculate differential cross

sections using

CTEQ5

following Gandhi

et al.

. For

interactions, the simulation of the

decay uses TAUOLA

29–

Neutrinoinduced cascades are reconstructed following

the procedure described in Sec. III. Position, zenith angle

and energy resolutions for a flux of

are calculated

using the difference distributions shown in Fig. 3. The posi

tion resolution is roughly4minthe

dimension and 5.5 m

and

for contained cascades.

Note that position reso

lution obtained with the pulsed laser is better than that pre

dicted for Cherenkov light because optical ice properties are

more favorable at the longer wavelength.

The reconstructed

position is biased in the direction of the cascade, but since

the mean of this shift is only about 2 m for contained cas

cades it has a negligible impact on the final result. Zenith

angle resolution is 25° –30° depending on the cascade en

ergy.

The energy reconstruction has a resolution of 0.12–0.20

in log

for contained cascades in the range 1 TeV–100

TeV, increasing as a function of cascade energy. Energy re

construction of contained cascades is possible from approxi

mately 50 GeV

the minimum energy cascade which can

trigger the detector

to about 100 TeV. At energies higher

than 100 TeV all, or almost all, of the OMs are hit and thus

energy reconstruction by the minimization of Eq.

is not

FIG. 2. Energy spectra of reconstructed atmospheric muon en

ergy losses for experimental data and standard simulated muon

background after application of selection criteria 1–9 from Table I.

Agreement between simulation and experimental data depends on a

combination of the simulated ice properties and the OM angular and

absolute sensitivity. These effects have been taken into account in

the calculation of systematic uncertainties in Sec. VI.

FIG. 3. The four plots show the difference between simulated and reconstructed vertex position, energy and direction of cascades. The

monoenergetic cascades have

10 TeV and are contained within the detector. Vertical scale for all four plots is arbitrary.

SEARCH FOR NEUTRINOINDUCED CASCADES WITH . . . PHYSICAL REVIEW D

, 012003

2003

0120035

possible.

Such highenergy events would, however, cer

tainly be identifiable, and probably they can be reconstructed

by other techniques.

V. ANALYSIS

A. Filter

The first step in the analysis is to apply an initial set of

selection criteria, here called the ‘‘filter,’’ which results in a

reduction of the data sample size by more than two orders of

magnitude. The filter first removes spurious hits arising from

electronic and PMT noise. It then uses the fast reconstruction

algorithms described earlier, a simple energy estimator, and

topological characteristics of the hit pattern to select poten

tial signal events. The various filter steps were tuned to reject

a simulated background of downgoing cosmicray muons.

After the filter has been applied, hits likely to have come

from crosstalk are removed, as explained below. Then each

event is reconstructed twice, first with a cascade hypothesis

and then with a muon hypothesis. Several selection criteria

are then applied to the data based on the results of the recon

struction.

Atmospheric

and

neutrinos are simulated according

to the flux calculated by Lipari

. Contributions to cas

cades from both atmospheric

CC and NC interactions

and

NC interactions

are taken into account. In the en

ergy range relevant to this analysis (

5 TeV), neutrino

oscillations are not important in the simulation of atmo

spheric neutrinos.

B. Removal of electronic crosstalk

Electronic crosstalk is present in the twisted pair cables

used for strings 5–10. Spurious hits arising from crosstalk

can degrade the reconstruction quality. Crosstalk is not in

cluded in the simulations, so its removal is an important facet

of this analysis.

We generate a detectorwide map of the crosstalk using

the pulsed laser. For each OM in strings 5–10, pulsed laser

data are taken in which only the PMT in the OM near the

laser diffuser ball has its high voltage enabled. Any hit in the

flashed OM is thus known to be due to light and any hit in

any other OM is known to be due to crosstalk. The cross

talk map identifies the pairs of crosstalkinducing and cross

talkinduced OMs as well as the correlation in time and am

plitude of real and crosstalk hits. The map shows that cross

talk occurs for OMs in the same string that are close

neighbors or for OMs in the same string that are separated by

150–200 m. The origin of crosstalk is correlated with the

relative positioning of individual electrical cables within the

string

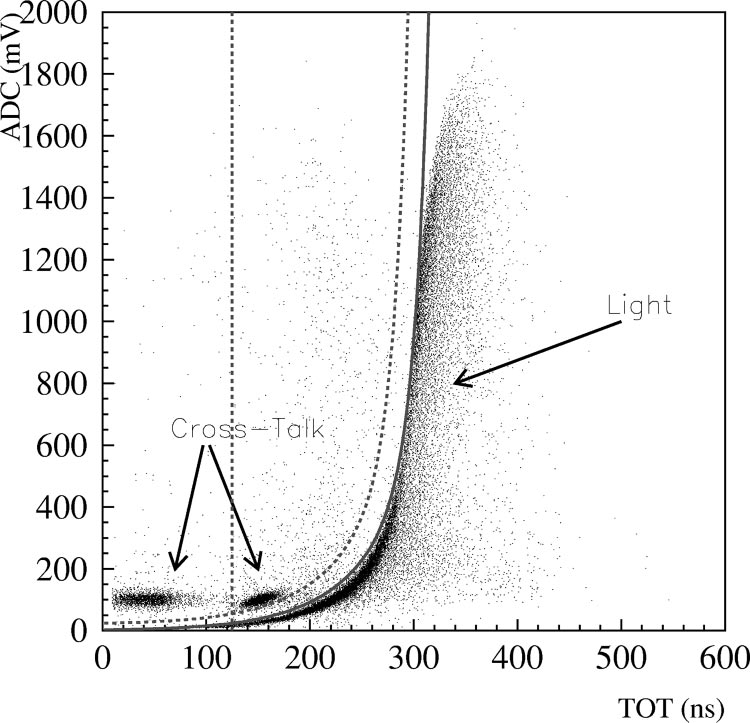
Crosstalk hits may also be characterized by narrowness

small time over threshold or ‘‘TOT’’

coupled with unex

pectedly large amplitude. Crosstalkinduced and light

induced hits lie in different regions of the amplitude vs TOT

space and may therefore be separated from one another. Fig

ure 4 shows the amplitude vs TOT distributions for both

types of hits.

The crosstalk map and the amplitude vs TOT information

are both used to remove crosstalk from the experimental

data.

C. Selection criteria

Table I lists the selection criteria and the passing rates for

experimental data and the various samples of Monte Carlo

calculations used in this analysis. Selection criteria which

have not already been described in Sec. III are described

below, followed by a physical justification for each criterion.

The ratio of the smallest to the largest eigenvalues of the

tensor of inertia of the position of the hits,

sphe

ricity

, is used to classify events.

Small values of the sphe

ricity correspond to hits located along a narrow cylinder, as

expected for a muon. Values of the sphericity close to unity

correspond to a spherical distribution of the hits, as expected

for contained cascades.

The dispersive nature of the ice and of the cables that

transmit the electrical signals from the OMs to the electron

ics on the surface render sharp signals in the ice into signifi

cantly broader pulses at the surface. For this reason, counting

the number of OMs with large TOT,

big TOT

, gives a rough

estimate of the energy of the event. For this analysis a TOT

is considered large if it exceeds the value estimated from

Monte Carlo simulations to correspond to one photoelectron

by at least a factor of 1.5. A contained cascade with 300 GeV

To calculate a tensor of inertia in this context, a unit mass is

hypothesized at each hit OM position.

FIG. 4. Amplitude vs time over threshold

TOT

distribution for

hits on OM 149 due to light and crosstalk. The data shown to the

right of the solid curve are generated using the pulsed laser with

only the high voltage for the PMT in OM 149 enabled

all other

PMTs had their high voltage disabled

. This region of the plot there

fore contains hits created by light. The data shown to the left of the

solid curve are also generated using the pulsed laser, but with a

diffuser ball located 200 m above OM 149, close to OM 129, in the

same string as OM 149. Only OM 129 had its high voltage enabled.

This region of the plot therefore contains hits in OM 149 due to

crosstalk. Hits are removed from an event if they lie to the left of

the dashed curve or if they have a TOT smaller than 125 ns

indi

cated by the dashed line

J. AHRENS

et al.

PHYSICAL REVIEW D

, 012003

2003

0120036

of energy corresponds roughly to

big TOT

The quality of the likelihood reconstruction is determined

from the reduced likelihood parameter, defined by

log

hits

fit

), where

fit

is the number of fitted pa

rameters. Lower values of

correspond to better reconstruc

tion quality.

A hit is considered

direct

if the time residual is between

15 ns and 75 ns. The number of direct hits,

dir

, is another

measure of the quality of the reconstruction. Both the single

and multiphotoelectron positiontime reconstruction report

the number of direct hits.

Criteria 1–5 of Table I correspond to the filter and these

criteria must be satisfied by all events in the analysis. The cut

big TOT

selects highenergy events, and the cut on the

sphericity selects events in which the hit topology is cascade

like. The cut on the speed of the line fit,

line

, removes easily

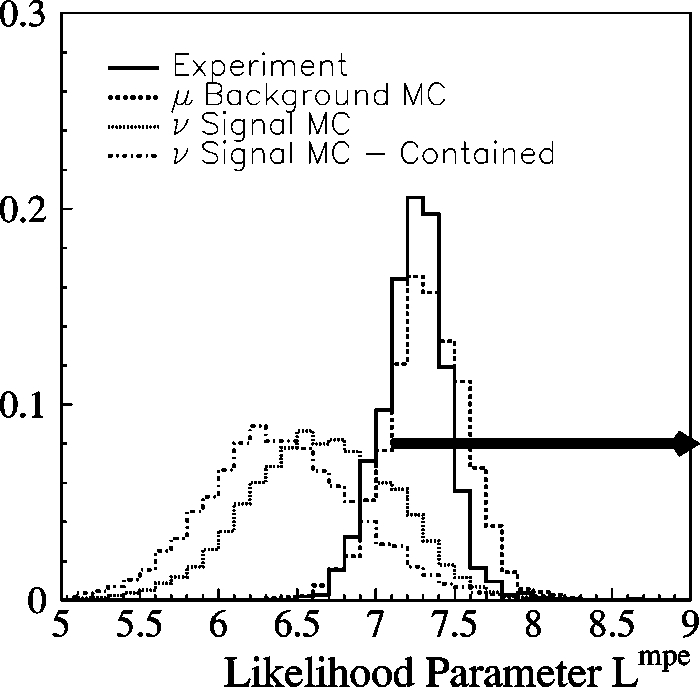
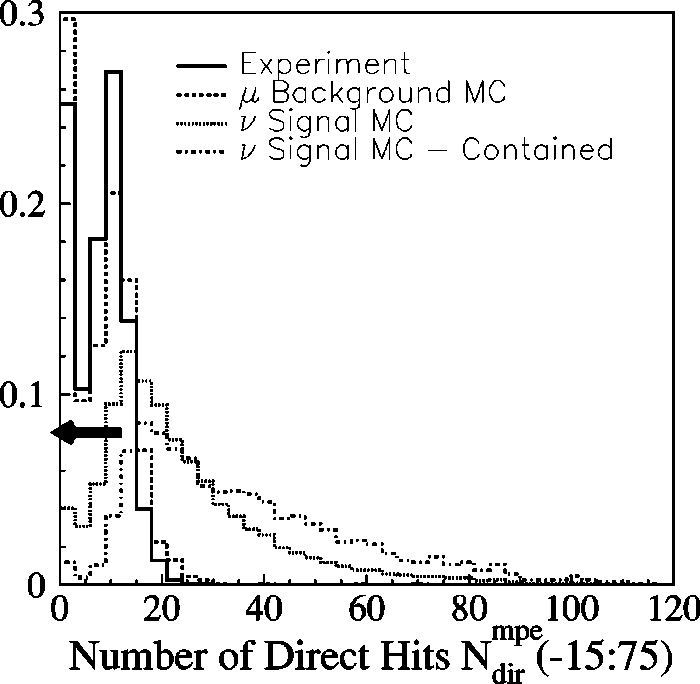
identified downgoing muons. As shown in Fig. 5 and Fig. 6,

cuts on the likelihood parameter

criterion 6

and the number

of direct hits

criterion 7

are used to eliminate noncascade

like events and preserve cascadelike events with good re

construction quality. In addition to the filter criteria, angular

cuts

criteria 8 and 10

are used to reduce clear muonlike

events and to select upgoing cascadelike events, and crite

rion 11 selects highenergy events within a given distance

from the vertical axis of the detector, where

is the recon

structed cascade energy using Eqs.

and

, and

mpe

(

mpe

)

(

mpe

)

Criterion 9 is discussed in detail be

low.

The filter was developed based strictly on the predictions

of the signal and background Monte Carlo simulations. As

more and more cuts were applied after the filter, it was found

that the experimental data and simulations disagreed in the

shape of the

component of the reconstructed cascade posi

tion and in the reconstructed cascade direction. Inadequately

simulated or unsimulated detector instrumentals, such as op

tical properties of the ice and crosstalk, contribute to this

disagreement. Restricting the regions of the detector used in

this analysis reduces the effective volume by more than a

factor of two, but restores the agreement between experimen

tal data and simulations. Moreover, the disagreement is also

present in the reconstructed cascade direction. Only the re

gions of the detector that are accepted, show agreement in

the reconstructed cascade direction. Events are accepted only

if their reconstructed vertices satisfy selection criterion num

ber 9:

80 m

40 mor40 m

160 m with re

spect to the center of the detector

located at 1730 m below

the surface

VI. SYSTEMATIC UNCERTAINTIES

There are several uncertainties inherent in estimating the

detector sensitivity to highenergy neutrinoinduced cas

cades. First, the detection medium is a natural material

South Pole ice

whose properties are not precisely known.

Second, there are no sufficiently powerful acceleratorbased

sources of neutrinos available for use as calibration beams.

Consequently, the understanding of the detector sensitivity is

achieved using downgoing atmospheric muons,

in situ

light

sources and Monte Carlo simulations.

To estimate the systematic uncertainty due to imprecise

knowledge of the optical properties of the ice, simulations

have been performed using the least and the most transparent

ice that we have measured at AMANDA depths. The cascade

sensitivity is modified by 20% using either extreme model of

the optical properties. Uncertainties in the bubble density in

the drillhole ice translate to uncertainties in the OM angular

sensitivity. Monte Carlo simulations with increased bubble

density in the drillhole ice degrade the cascade sensitivity

FIG. 5. Normalized distribution of the reduced likelihood pa

rameter

mpe

for experimental data

solid line

, background atmo

spheric

simulation

dashed line

simulation assuming an

power law spectrum

dotted line

and contained

simulation as

suming an

power law spectrum

dotteddashed line

. Con

tained events have their vertices in a cylinder 400 m in height and

60 m in radius, roughly matching the detector dimensions. Selection

criteria 1–5 from the same table have already been applied to all the

samples shown. The arrow indicates the region removed by cut 6

from Table I.

FIG. 6. Normalized distribution of direct hits for experimental

data

solid line

, background atmospheric

simulation

dashed

line

simulation assuming an

power law spectrum

dotted

line

and contained

simulation assuming an

power law spec

trum

dotteddashed line

. Contained events have their vertices in a

cylinder 400 m in height and 60 m in radius, roughly matching the

detector dimensions. Selection criteria 1–5 from the same table

have already been applied to all the samples shown. The arrow

indicates the region removed by cut 7 from Table I.

SEARCH FOR NEUTRINOINDUCED CASCADES WITH . . . PHYSICAL REVIEW D

, 012003

2003

0120037

by 9%. The absolute sensitivity of the OMs is also uncertain

at the level of 40%. Monte Carlo simulations with altered

absolute OM sensitivity modifies the cascade sensitivity by

5%. This dependence is weak due to the high

hits

require

ment imposed by this analysis.

The dependence is much

stronger at earlier stages of the analysis, where the average

hits

is much lower. For example, before the filter is applied

a variation in absolute OM sensitivity of 40% results in a

modification of the cascade sensitivity by roughly 35%.

Crosstalk can reduce the sensitivity of the detector to

highenergy neutrinoinduced cascades. Events for which

crosstalk is not fully removed are typically mis

reconstructed and are therefore unlikely to have sufficient

quality to pass our selection criteria. The pulsed laser data is

used to estimate the cascade sensitivity loss due to crosstalk

for different locations in the detector. These studies indicate

that the sensitivity is degraded by 7% due to crosstalk.

This

7% degradation is applied directly to the limit and not treated

as a systematic uncertainty.

Related to crosstalk is the un

certainty in the limits due to using slices in

. Changing

each boundary of the slices by the position resolution in

modifies the cascade sensitivity by 4%.

Uncertainties in the limits due to neutrinonucleon cross

sections, total cascade light output, and cascade longitudinal

development have also been estimated using Monte Carlo

simulations. For each of these cases the cascade sensitivity is

modified by

5%.

The systematic uncertainties discussed so far are added in

quadrature, giving an overall systematic uncertainty on the

sensitivity of 25%. We follow the procedure described in

34,35

to determine how to modify the final limit in light of

this systematic uncertainty, assuming that the uncertainties

are of a Gaussian nature.

The spectrum of cascadelike events produced by down

going muons is shown in Fig. 2

see also Sec. IV B

. Stan

dard simulations as well as simulations with modified ice

properties and OM angular and absolute sensitivities have

been performed. The disagreement between experiment and

simulations may be explained by the uncertainties in the

knowledge of the optical properties of ice, the OM sensitiv

ity, the cosmicray spectrum and the rate of muon energy

losses. From Fig. 2 it can be seen that reasonable agreement

between experiment and simulations is restored by shifting

the energy scale by up to 0.2 in log

. This uncertainty in

the energy scale results in an uncertainty on the sensitivity of

less than 25%. This uncertainty is

not

independent of the

other sources of systematic uncertainty that we have studied.

It demonstrates, however, that the overall systematic uncer

tainty has not been grossly under or overestimated.

VII. RESULTS

The analysis is applied to simulated samples of atmo

spheric

and

background, highenergy neutrino signal

all flavors

, and atmospheric muons, and to the 1997 experi

mental data set. In the experimental data zero events are

found. The simulation of atmospheric

predicts 0.01

events, and the simulation of atmospheric

predicts 0.01

events from NC interactions

both these numbers have been

rounded up from distinct smaller values

. Zero events are

found in the simulated atmospheric muon sample after all

cuts. A limit on the flux of neutrinos assuming an

power

law spectrum is set using the following formula:

90%

(

tot

eff

where

is the neutrino flavor,

the neutrino energy,

the

neutrino zenith angle,

90%

2.62 determined using the uni

fied FeldmanCousins procedure

with a correction ap

plied for the estimated 25% systematic uncertainty

34,35

the live time

130.1 days

Avogadro’s number,

ice

the

density of ice,

tot

(

) the neutrino cross section

eff

(

) the effective volume of the detector

see Table II

the fraction of the total neutrino flux comprised by the

neutrino flavor

, and

(

) a function that corrects the flux

for Earth absorption and NC scattering. The integration of

Eq.

has been done for neutrino energies between 5 TeV

and 300 TeV.

The 90% C.L. limit on the diffuse flux of

for neutrino energies between 5 TeV and 300

TeV, assuming a neutrino flux ratio of 1:1:1 at the detector, is

9.8

GeV cm

The 90% C.L. limit on the diffuse flux of

for neutrino

energies between 5 TeV and 300 TeV is

6.5

GeV cm

The latter limit is independent of the assumed neutrino flux

ratio. The limits without incorporating the effects of system

atic uncertainties are 9.1

GeV cm

and 6.1

GeV cm

1sr

, respectively.

Note that since the

limit in Eq.

is on the sum of the fluxes of all neutrino

flavors, and the limit in Eq.

is on an individual flavor, the

former limit should be divided by a factor of three to com

pare it properly to the latter.

Our results together with other limits on the flux of dif

fuse neutrinos are shown in Fig. 8. Since recent results from

other low energy neutrino experiments

1–4

indicate that

highenergy cosmological neutrinos will have a neutrino fla

J. AHRENS

et al.

PHYSICAL REVIEW D

, 012003

2003

0120038

vor flux ratio of 1:1:1 upon detection, in this figure we scale

limits derived under different assumptions accordingly. For

example, to do a sidebyside comparison of a limit on the

flux of

, derived under the as

sumption of a ratio of 1:1:1, to a limit on just the flux of

, the latter must be degraded by a factor of three.

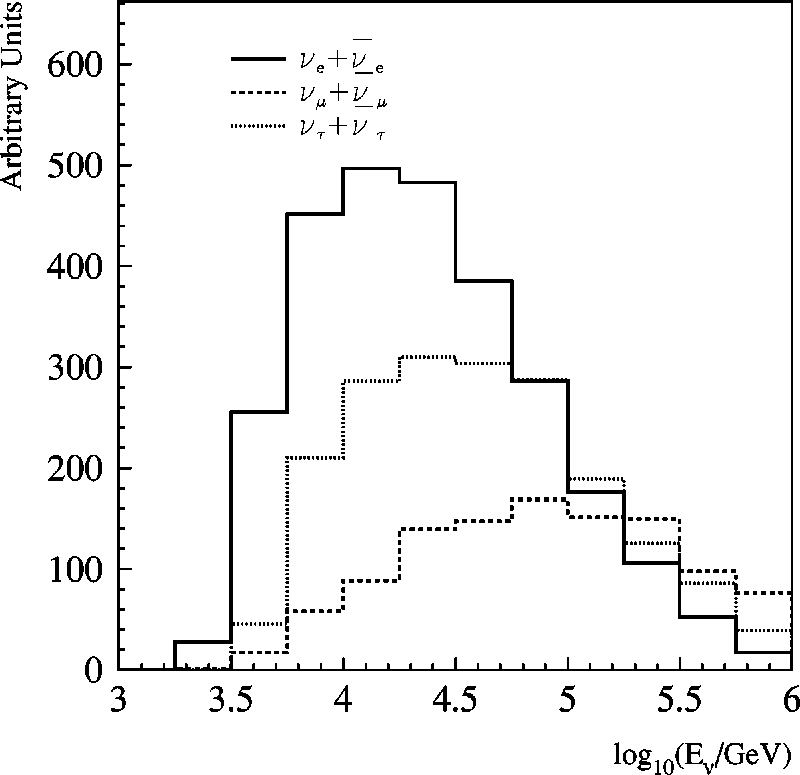
FIG. 7. Distribution of

and

energies after all selection

criteria have been applied. The relative normalization between the

histograms indicates the relative number of events for each neutrino

flavor that passes all the selection criteria. The initial energy distri

bution follows an

spectrum. Neutrino absorption inside Earth,

NC scattering and

decay have been taken into account as de

scribed in Sec. IV C.

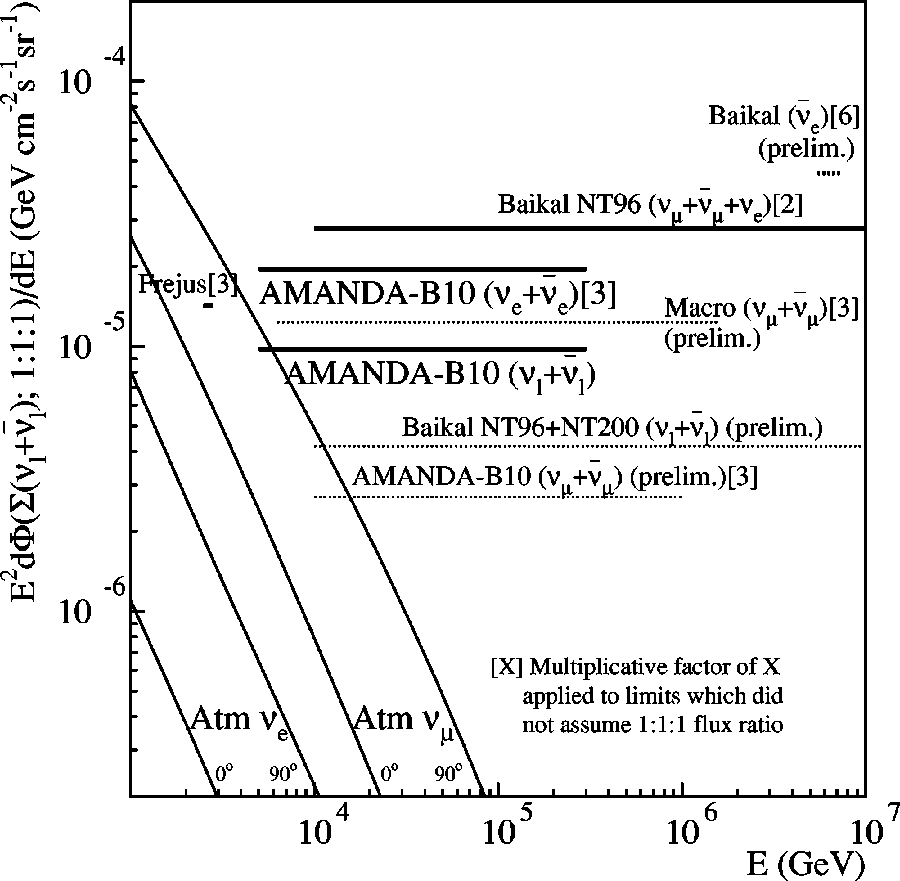
FIG. 8. The limits on the cascadeproducing neutrino flux,

summed over the three active flavors, presented in this work and in

other experiments, with multiplicative factors applied as indicated

to permit comparison of limits derived with different assumed neu

trino fluxes at the detector: Baikal (

)

at the

resonance

;

Baikal NT96 (

)

; Frejus (

)

; MACRO

(

)

; Baikal NT96

NT200 (

)

38,42

;

AMANDAB10 (

)

. Also shown are the predicted hori

zontal and vertical

and

atmospheric fluxes

TABLE II. Effective volume, in units of 10

, for all neutrino flavors as a function of energy and

zenith angle after all the selection criteria have been applied. Uncertainties are statistical only.

3.0–10.0 TeV 10.0–30 TeV 30–100 TeV 100–300 TeV

cos

0.6 0.80

0.05 1.85

0.10 1.87

0.15 1.37

0.20

0.6

cos

0.2 0.40

0.03 0.85

0.07 1.10

0.10 0.72

0.10

0.2

cos

0.2 0.08

0.01 0.22

0.02 0.36

0.05 0.31

0.07

cos

0.6 0.82

0.05 1.67

0.12 1.85

0.10 1.60

0.15

0.6

cos

0.2 0.42

0.03 0.77

0.07 0.92

0.07 0.74

0.10

0.2

cos

0.2 0.09

0.01 0.20

0.02 0.35

0.05 0.30

0.07

cos

0.6 0.08

0.02 0.35

0.05 0.87

0.1 1.27

0.15

0.6

cos

0.2 0.05

0.01 0.25

0.03 0.70

0.10 1.60

0.10

0.2

cos

0.2 0.05

0.01

cos

0.6 0.12

0.02 0.34

0.05 0.70

0.05 1.17

0.15

0.6

cos

0.2 0.05

0.01 0.25

0.03 0.70

0.1 0.14

0.01

0.2

cos

0.2 0.03

0.01

cos

0.6 0.35

0.05 1.10

0.10 1.85

0.15 1.35

0.20

0.6

cos

0.2 0.15

0.03 0.50

0.05 0.85

0.10 1.05

0.10

0.2

cos

0.2 0.04

0.01 0.10

0.02 0.23

0.05 0.32

0.07

cos

0.6 0.35

0.05 1.15

0.10 1.65

0.10 1.50

0.15

0.6

cos

0.2 0.15

0.03 0.45

0.05 0.80

0.10 1.20

0.10

0.2

cos

0.2 0.06

0.01 0.12

0.02 0.22

0.04 0.31

0.06

SEARCH FOR NEUTRINOINDUCED CASCADES WITH . . . PHYSICAL REVIEW D

, 012003

2003

0120039

N.B.: We assume that

::1:1.

Following the Learned and

Mannheim prescription for presenting limits

, we show

neutrino energy distributions after applying all the selection

criteria in Fig. 7.

It should be noted that most searches of diffuse fluxes

shown in Fig. 8 are based on the observation of upgoing

neutrinoinduced muons. Only Baikal and AMANDA have

presented limits from analyses that search for neutrino

induced cascades and only the AMANDA analysis uses full

cascade event reconstruction.

VIII. CONCLUSIONS

Highenergy neutrinoinduced cascades have been

searched for in the data collected by AMANDAB10 in

1997. Detailed event reconstruction was performed. Using

situ

light sources and atmospheric muon catastrophic energy

losses, the sensitivity of the detector to highenergy cascades

has been demonstrated.

No evidence for the existence of a diffuse flux of neutri

nos producing cascade signatures has been found. Effective

volumes as a function of energy and zenith angle for all

neutrino flavors have been presented. The effective volumes

allow the calculation of limits for any predicted neutrino flux

model. The limit on cascades from a diffuse flux of

(

)

9.8

GeV cm

assuming a neutrino flavor flux ratio of 1:1:1 at the

detector. The limit on cascades from a diffuse flux of

(

)

6.5

GeV cm

, inde

pendent of the assumed neutrino flux ratio. The limits are

valid for neutrino fluxes in the energy range of 5 TeV to 300

TeV.

ACKNOWLEDGMENTS

This research was supported by the following agencies:

U.S. National Science Foundation, Office of Polar Programs;

U.S. National Science Foundation, Physics Division; Univer

sity of Wisconsin Alumni Research Foundation; U.S. Depart

ment of Energy; Swedish Natural Science Research Council;

Swedish Research Council; Swedish Polar Research Secre

tariat; Knut and Alice Wallenberg Foundation, Sweden; Ger

man Ministry for Education and Research; U.S. National En

ergy Research Scientific Computing Center

supported by

the Office of Energy Research of the U.S. Department of

Energy

; UCIrvine AENEAS Supercomputer Facility; Deut

sche Forschungsgemeinschaft

DFG

. D.F.C. acknowledges

the support of the NSF CAREER program and C.P. de los H.

acknowledges support from the EU 4th framework of Train

ing and Mobility of Researchers.

Q. Ahmad

et al.

, Phys. Rev. Lett.

, 071301

2001

Q. Ahmad

et al.

, Phys. Rev. Lett.

, 011301

2002

Q. Ahmad

et al.

, Phys. Rev. Lett.

, 011302

2002

S. Fukuda

et al.

, Phys. Rev. Lett.

, 3999

2000

E. Andre

et al.

, Nature

London

410

, 441

2001

J. Ahrens

et al.

, Phys. Rev. D

, 012005

2002

J. Ahrens

et al.

, Phys. Rev. D

, 032006

2002

F. Halzen and D. Saltzberg, Phys. Rev. Lett.

, 4305

1998

S. Dutta

et al.

, Phys. Rev. D

, 113015

2001

J. Beacom

et al.

, Phys. Rev. D

, 021302

2002

T. Stanev, Phys. Rev. Lett.

, 5427

1999

C. Wiebusch, Ph.D. thesis, RWTH Aachen, Aachen, Germany,

1995.

G. Hill and M. Leuthold, in Proceedings of the 27th Interna

tional Cosmic Ray Conference, Hamburg, Germany, 2001, p.

1113.

G. Hill, in Proceedings of the 26th International Cosmic Ray

Conference, Salt Lake City, 1999, HE.6.3.02.

B. Price

et al.

, Geophys. Res. Lett.

, 2129

2000

V. Stenger, DUMAND Internal Report HDC190, 1990.

C. Wiebusch, DESYZeuthen, Germany, 1998, DESYproc

199901.

M. Kowalski and I. Taboada, in Proceedings of 2nd Workshop

Methodical Aspects of Underwater/Ice Neutrino Telescopes,

Hamburg, Germany, 2001.

M. Kowalski, Diploma thesis, Humboldt University, Berlin,

Germany, 2000.

I. Taboada, Ph.D. thesis, University of Pennsylvania, Philadel

phia, 2002.

E. Andre

et al.

, Astropart. Phys.

2000

D. Heck

et al.

, Tech. Rep. FZKA 6019, Forshungszebtrum

Karlsruhe, Karlsruhe, Germany, 1998.

N. Kalmykov

et al.

, Nucl. Phys. B

Proc. Suppl.

52B

,17

1997

B. WiebelSooth

et al.

, astroph/9709253.

W. Lohmann

et al.

, CERN Yellow Report CERN8503, 1985.

R. Kopp

et al.

private comunication

A. Dziewonski and D.L. Anderson, Phys. Earth Planet. Inter.

, 297

1981

R. Gandhi

et al.

, Phys. Rev. D

, 093009

1999

S. Jadach, J. Kuhn, and Z. Was, Comput. Phys. Commun.

275

1990

M. Jezabek, Z. Was, S. Jadach, and J. Kuhn, Comput. Phys.

Commun.

,69

1992

S. Jadach, Z. Was, R. Decker, and J. Kuhn, Comput. Phys.

Commun.

, 361

1993

P. Lipari, Astropart. Phys.

, 193

1993

J. Klug, Diploma thesis, Uppsala University, Sweden, 1997.

J. Conrad, O. Botner, A. Hallgren, and C. Perez de los Heros,

this issue, Phys. Rev. D

, 012002

2003

J. Conrad, O. Botner, A. Hallgren, and C. Perez de los Heros,

Proceedings of Advanced Statistical Techniques in Particle

Physics, Durham, 2002, hepex/0206034.

G.J. Feldman and R.D. Cousins, Phys. Rev. D

, 3873

1998

J. Learned and K. Mannheim, Annu. Rev. Nucl. Part. Sci.

679

2000

V. Balkanov

et al.

, in Proceedings of the 9th International

Workshop on Neutrino Telescopes, Venice, Italy, 2001, Vol. II,

p. 591, astroph/0105269.

V. Balkanov

et al.

, Astropart. Phys.

,61

2000

W. Rhode

et al.

, Astropart. Phys.

, 217

1994

L. Perrone

et al.

, in Proceedings

, p. 1073.

Baikal Collaboration, J. Dzhilkibaev

private communication

J. AHRENS

et al.

PHYSICAL REVIEW D

, 012003

2003

01200310