doi:10.1016/j.astropartphys.2004.09.008

Flux limits on ultra high energy neutrinos

with AMANDA-B10

M. Ackermann

, J. Ahrens

, H. Albrecht

, D. Atlee

, X. Bai

, R. Bay

M. Bartelt

, S.W. Barwick

, T. Becka

, K.H. Becker

, J.K. Becker

E. Bernardini

, D. Bertrand

, D.J. Boersma

,S.Bo

ser

, O. Botner

A.Bouchta

,O.Bouhali

,J.Braun

,C.Burgess

,T.Burgess

,T.Castermans

D. Chirkin

, T. Coarasa

, B. Collin

, J. Conrad

, J. Cooley

, D.F. Cowen

A.Davour

,C.DeClercq

,T.DeYoung

,P.Desiati

,P.Ekstro

,T.Feser

T.K. Gaisser

, R. Ganugapati

, H. Geenen

, L. Gerhardt

, A. Goldschmidt

A. Groß

, A. Hallgren

, F. Halzen

, K. Hanson

, D. Hardtke

, R. Hardtke

T. Harenberg

, T. Hauschildt

, K. Helbing

, M. Hellwig

, P. Herquet

G.C. Hill

, J. Hodges

, D. Hubert

, B. Hughey

, P.O. Hulth

, K. Hultqvist

S. Hundertmark

, J. Jacobsen

, K.H. Kampert

, A. Karle

, J. Kelley

M. Kestel

,L.Ko

pke

, M. Kowalski

, M. Krasberg

, K. Kuehn

, H. Leich

M. Leuthold

, J. Lundberg

, J. Madsen

, K. Mandli

, P. Marciniewski

H.S. Matis

, C.P. McParland

, T. Messarius

, Y. Minaeva

, P. Mioc

inovic

R. Morse

, S. Movit

,K.Mu

nich

, R. Nahnhauer

, J.W. Nam

T. Neunho

ffer

, P. Niessen

, D.R. Nygren

,H.O

gelman

, Ph. Olbrechts

C. Pe

rez de los Heros

, A.C. Pohl

, R. Porrata

, P.B. Price

, G.T. Przybylski

K. Rawlins

, E. Resconi

, W. Rhode

, M. Ribordy

, S. Richter

J. Rodrı

guez Martino

, D. Rutledge

, H.G. Sander

, K. Schinarakis

S. Schlenstedt

, D. Schneider

, R. Schwarz

, A. Silvestri

, M. Solarz

G.M. Spiczak

, C. Spiering

, M. Stamatikos

, D. Steele

, P. Steffen

R.G. Stokstad

, K.H. Sulanke

, I. Taboada

, O. Tarasova

, L. Thollander

S. Tilav

, L.C. Voicu

, W. Wagner

, C. Walck

, M. Walter

, Y.R. Wang

C.H. Wiebusch

, R. Wischnewski

, H. Wissing

, K. Woschnagg

, G. Yodh

0927-6505/$ - see front matter

doi:10.1016/j.astropartphys.2004.09.008

Corresponding author.

E-mail address:

stephan.hundertmark@physto.se(S. Hundertmark).

Astroparticle Physics 22 (2005) 339–353

www.elsevier.com/locate/astropart

DESY, 15735 Zeuthen, Germany

Institute of Physics, University of Mainz, D-55099 Mainz, Germany

Department of Physics, Pennsylvania State University, University Park, PA 16802, USA

Bartol Research Institute, University of Delaware, Newark, DE 19716, USA

Department of Physics, University of California, Berkeley, CA 94720, USA

Department of Physics, Bergische Univerita

t Wuppertal, 42097 Wuppertal, Germany

Department of Physics and Astronomy, University of California, Irvine, CA 92697, USA

Universite

Libre de Bruxelles, Science Faculty CP230, Boulevard du Triomphe, B-1050 Brussels, Belgium

Division of High Energy Physics, Uppsala University, S-75121 Uppsala, Sweden

Department of Physics, University of Wisconsin, Madison, WI 53706, USA

Department of Physics, Stockholm University, SE-10691 Stockholm, Sweden

University of Mons-Hainaut, 7000 Mons, Belgium

Vrije Universiteit Brussel, Dienst ELEM, B-1050 Brussels, Belgium

Department of Physics, University of Maryland, College Park, MD 20742, USA

Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA

Physics Department, University of Wisconsin, River Falls, WI 54022, USA

Department of Chemistry and Biomedical Sciences, University of Kalmar, S-39182 Kalmar, Sweden

Department of Physics, Universidad Simo

n Bolı

var, Caracas, 1080, Venezuela

Received 17 August 2004; received in revised form 22 September 2004; accepted 30 September 2004

Available online 13 November 2004

Abstract

Data taken during 1997 with the AMANDA-B10 detector are searched for a diffuse flux of neutrinos of all flavors

with energies above 10

eV. At these energies the Earth is opaque to neutrinos, and thus neutrino induced events are

concentrated at the horizon. The background are large muon bundles from down-going atmospheric air shower events.

No excess events above the background expectation are observed and a neutrino flux following

, with an equal mix

of all flavors, is limited to

(10

eV <

eV)

0.99

GeVcm

at 90% confidence level. This

is the most restrictive experimental bound placed by any neutrino detector at these energies. Bounds to specific extra-

terrestrial neutrino flux predictions are also presented.

PACS:

95.55.Vj; 95.85.Ry; 96.40.Tv

Keywords:

Neutrino telescopes; Neutrino astronomy; UHE neutrinos; AMANDA

1. Introduction

Neutrino telescopes like AMANDA [1] are uni-

que astronomy tools, originally designed to look

downwards for Cherenkov light emitted by up-

ward traveling muons from charged-current

muon–neutrino interactions. The Earth is used to

filter the muon flux from cosmic ray air showers.

As muons cannot pass through the Earth, any up-

ward traveling muon in the vicinity of the detector

is neutrino induced. Due to the sparse instrumen-

tation of the detection medium and the optical

properties of the medium itself, misidentification

of the direction of the muon by the reconstruction

algorithm is possible. To reduce the amount of

down-going muons, and therefore the probability

for misidentification, these detectors are located

under as much overburden as feasible.

As the energy of the neutrino increases, the neu-

trino–nucleon cross section and the muon range

grow. Both effects result in a large detection prob-

ability for high energy neutrinos. Above 40TeV,

the Earth diameter exceeds the neutrino charged-

current interaction length and high energy neutri-

340

M. Ackermann et al. / Astroparticle Physics 22 (2005) 339–353

nos are significantly absorbed

[2].At UHE

the

Earth is essentially opaque to muon- and elec-

tron–neutrinos[3]and only downward to horizon-

tally traveling neutrinos can be detected. The

overburden above the AMANDA detector is lim-

ited, which limits the interaction probability for

neutrinos, concentrating the muons from UHE

neutrinos at the horizon. Klein and Mann[3]esti-

mate that a few muons per year above 10

from UHE neutrino sources might be detected

with an 0.1km

detector, an effective area that is

achieved by this analysis (as shown in[4]). The en-

ergy range above 10

eV is interesting, as experi-

mentally there are currently no strong limits on

neutrino fluxes from models describing active

galactic nuclei (AGN) at these energies. At higher

energies, above 10

eV, one expects the guaran-

teed flux of neutrinos from interactions of high

energy cosmic rays with the cosmic microwave

background, or the more speculative flux from de-

cays of topological defects (for an overview see

[5–7]). Cosmological sources are expected to pro-

duce neutrinos in pp or p

collisions, resulting in

a flavor ratio of

= 1:2:0 at the source. As

these neutrinos propagate over cosmological dis-

tances, oscillations between the different flavors re-

sult in a ratio at Earth of

= 1:1:1 [8].

Therefore all three flavors are initially of the same

importance for detection, but for muon–neutrinos

the detection probability is higher, due to the long

path length of the resulting muons.

The search for a neutrino signal in the upper

hemisphere has to be performed in the presence

of the large flux of down-going atmospheric muon

bundles. This analysis exploits the fact that these

events have different characteristics than neutrino

induced events. The primary cosmic ray spectrum

(protons and heavier elements) falls rapidly with

energy, following approximately

2.7

below the

knee and steepening thereafter to

3.1

. An atmo-

spheric air shower produced by an UHE primary

particle results in a muon bundle consisting of

hundreds to thousands of muons. At 10

–

eV approximately 90% of the primary energy

is consumed by the electromagnetic cascade of

the air shower and only a fraction of the remaining

energy is carried by the resulting muons[9]. When

comparing a single muon and a muon bundle of

the same energy, the bundle spreads the generated

Cherenkov light over a larger volume. In the detec-

tor, both classes of events can result in a large

number of photomultiplier tubes (PMT) being hit

by photons, but neutrino induced events have

more photon hits overall, i.e. more multiple hits

are found in single PMTs. Often, however, single

photons cannot be resolved. This can be compen-

sated for by exploiting the afterpulse behavior of

the PMTs. Each photoelectron has a small proba-

bility to generate an afterpulse delayed by several

microseconds. These afterpulses are used as a

‘‘low gain’’ outlet to identify high energy events

with a large number of photons incident on the

PMT. Using this and other event properties, it is

possible to reduce the number of events caused

by down-going atmospheric muons to a level

where a search for a signal from UHE neutrinos

becomes feasible. In[4]and[10]part of the data

taken in 1997 with the AMANDA-B10 array was

used to establish this technique and a preliminary

limit was set. In this analysis an improved neutrino

simulation is used, selection criteria are refined,

systematic uncertainties are assessed and the anal-

ysis is applied to the full 1997 data set.

2. The AMANDA-B10 detector

The data used in this analysis were taken with

the AMANDA-B10 detector [1] in 1997. This

detector consists of 302 Optical Modules (OMs)

on 10 vertical strings. The instrumented parts of

the strings are located between 1500m and

2000m below the South Pole ice surface. The

strings are arranged in two concentric circles.

The outer circle with a diameter of 120m is formed

by six strings equipped with a total of 216 OMs

connected to the surface via twisted pair cables.

The vertical separation of the OMs located on

these strings is 10m. Three strings lie on a 60m

diameter inner circle, the remaining string being

located at the center. These strings use coaxial

cable to connect 86 OMs, with 20m spacing, to

the surface. The coaxial or twisted pair cable

ltra

igh

nergy is used here for energies above 10

eV.

M. Ackermann et al. / Astroparticle Physics 22 (2005) 339–353

341

supplies the PMT inside the OM-pressure-sphere

with high voltage power and transmits the signal

to the amplifier and data acquisition electronics

(DAQ) located at the surface. The electrical signal

from the PMT is dispersed in the cable, which

strongly limits the capability to resolve single pho-

tons arriving at the PMT separated by less than a

few hundred nanoseconds. The PMT and/or the

amplifier saturate when more than some tens of

photoelectrons are generated in the PMT. Each

photoelectron produces an afterpulse with an

approximately 3% probability, well separated by

approximately 6

s from the initial pulse. These

late afterpulses appear when residual gas mole-

cules, ionized by electrons from the electron multi-

plier, travel back to the cathode and release

additional electrons

[11,12]. The AMANDA-B10

detector and its response to a simulated horizontal

eV muon is shown in Fig. 1.

3. Signal and background simulations

3.1. UHE neutrino simulation

The neutrino generator ANIS

[13]

is used to

generate neutrinos and anti-neutrinos of all flavors

following an

spectrum between 10

eV and

eV. All relevant standard model processes,

like charged- and neutral-current

N interactions,

resonant

scattering and tau–neutrino regener-

ation are simulated. Cross-sections are evaluated

up to 10

eV following the framework of pQCD

and with structure functions according to CTEQ5.

The neutrinos are propagated through the Earth

with a density profile taken from the Preliminary

Reference Earth Model

[14]. In case of a

charged-current interaction in the vicinity of the

detector, the resulting lepton and hadronic energy

deposition is simulated. Throughout this paper a

neutrino flavor ratio at Earth of

= 1:1:1

and a ratio of

is assumed. The events,

generated by ANIS, are re-weighted to a diffuse

AGN-like flux

=10

GeVcm

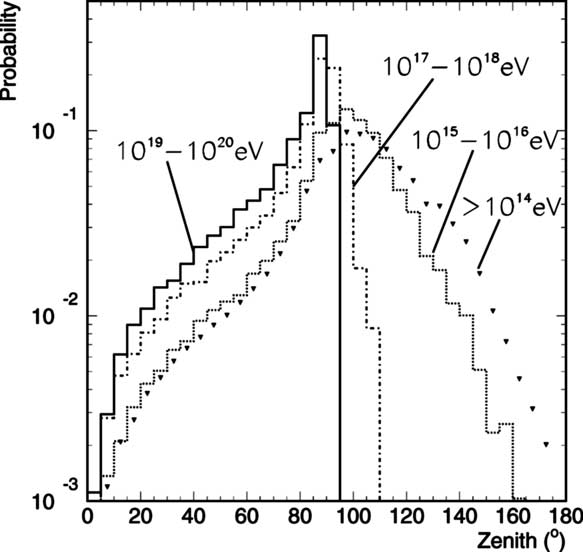
other UHE neutrino flux predictions.Fig. 2shows

the zenith angle distribution for muon–neutrinos

which underwent a charged-current interaction

within the muon path length from the detector.

With increasing neutrino energy, the absorption

of the neutrino flux becomes stronger and the

resulting muon flux concentrates near the horizon.

The event selection is developed using a simpler

single muon simulation, re-weighted to an

neutrino spectrum. In this simulation the Earth is

assumed to have the density of ice and the hadro-

nic energy deposition from the charged-current

interaction is neglected. Nevertheless, this simpli-

fied simulation leads to a good agreement in the

Fig. 1. A simulated horizontal 2

eV muon passes the

AMANDA-B10 detector. The different colors of the OMs

correspond to different hit times from yellow (early) to blue

(late). Only the hits depicted in yellow, orange and red are

generated by the muon, while the green and blue colored hits

are caused by afterpulses. In this event, all working OMs are hit

and nearly all of them report at least one hit from afterpulsing.

(For interpretation of the references in color in this figure

legend, the reader is referred to the web version of this article.)

The production of high energy

is suppressed in

interactions, altering the ratio

. For a discussion

of this effect see [35].

342

M. Ackermann et al. / Astroparticle Physics 22 (2005) 339–353

final neutrino energy and angular distributions

when compared to the results using the ANIS

generator.

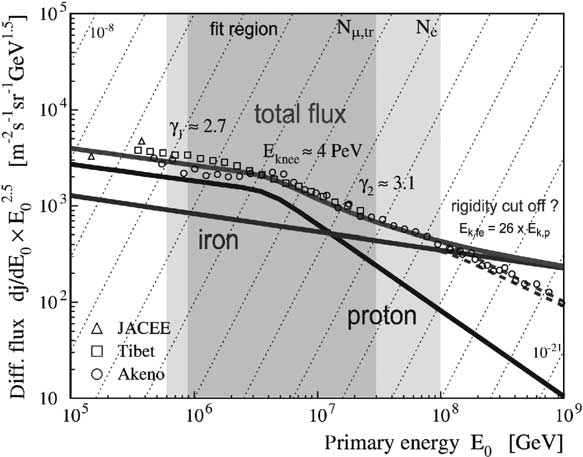
3.2. Cosmic ray air shower generation

Cosmic ray air showers are generated using the

CORSIKA program (version 5.7001, 1988)

[15]

with the QGSJET interaction model. To develop

the selection criteria, two sets of simulations are

performed. The first uses the primary composition

and the spectral slopes for the individual elements

from

[16], with energies of the primary particles

ranging from 8

eV to 10

eV. This simula-

tion corresponds to the standard AMANDA

background simulation. The second set is tailored

to more efficiently simulate events generated by

high energy primaries. Protons and iron primaries

are sampled from an

spectrum from

eV to 10

eV. Events resulting from

315

proton- and 145

iron-primaries

are re-weighted to the model taken from

[17],

which is shown in

Fig. 3. This model describes

the averaged measured primary cosmic ray flux

with proton and iron primaries. As the developed

selection criteria reject events generated by low en-

ergy primaries, the higher energy threshold and the

softer spectral slope allows to reduce the required

cpu time while generating a large number of high

energy air shower events.

3.3. Lepton propagation

Muons and taus produced in charged-current

neutrino interactions are propagated through

the ice and rock using MMC

[18]

while for

muons generated in cosmic ray air showers an

algorithm developed by Lipari and Stanev

[19]

is used. The simulation takes into account the re-

sponse of the detector to additional Cherenkov

photons generated by energy depositions due to

ionization and radiative processes. Table 1 shows

the mean path length of muons in ice as evalu-

ated with the algorithm presented in

[19].At

Fig. 3. The two-component model describing the averaged

measured primary cosmic ray flux taken from[17]is used to

simulate the cosmic ray air shower events.

Fig. 2. Zenith angle distribution for muon–neutrinos which

produced a muon able to reach the detector (A zenith angle of

180

corresponds to a upward-going particle). The probability

distribution is shown for a muon–neutrino flux following

and energies above 10

eV and between 10

–10

eV, 10

–

eV and 10

–10

eV.

Table 1

The mean path length for muons (

) with energies from

eV to 10

(eV) 10

(kmwe) 17 21 26 30 33 37

M. Ackermann et al. / Astroparticle Physics 22 (2005) 339–353

343

UHE energies, muons can travel up to several

tens of kilometers, which allows to monitor large

volumes of ice.

4. Data selection and analysis

During the 1997 data taking period a total of

1.05

events satisfied a majority trigger of at

least 16 hit OMs within about 2

s. The data tak-

ing rate was 100Hz. Out of the 302 OMs, 41

(14%) were either not functioning or showed

abnormal behavior and were excluded from the

analysis. Signals with a short time over threshold

(TOT) are mostly caused by electrical cross talk

between OMs on the same string and are removed

from the analysis. In order to enhance high energy

events, events that deposited a large amount of

photons in and around the detector are selected

by requiring hits in more than 95 OMs, with four

of them located on the inner strings. During the

detector

s operational time of 174 days, 4

events fulfilling these criteria were collected. Tak-

ing into account the detector dead time of 25%

the data taking period corresponds to 131 days

of live time. The goal of this analysis is to reject

atmospheric air shower events and retain a maxi-

mum number of UHE neutrino induced events.

Due to the long path length of UHE muons (see

Table 1), it is expected that events caused by

muon–neutrinos contribute a larger fraction to

the final event sample than electron– or tau–neu-

trino induced events. The development of selection

criteria is therefore performed with simulated

muon–neutrino induced events and only for the

optimization of the final criterion the electron–

and tau–neutrino induced events are added to

the analysis.

4.1. Variables

To separate UHE neutrino induced signal

events from air shower induced background events

eight variables are used. Two neural nets (NN)

combine subsets of these variables to achieve bet-

ter separation. The variables are defined as

follows:

NCHis the number of OMs that reported one

or more hits. The time-to-digital converters con-

nected to each OM can distinguish up to eight hits.

The variable NHITS is the sum of all hits for all

OMs.

Fig. 4(left) shows the NHITS distribution

of the experiment, air shower and signal simula-

tions. The atmospheric air shower simulation

describes the experimental data well, while the sig-

nal simulation extends to larger values of NHITS.

For bright events with many photons arriving at

the OM, dispersion of the electrical signal in the

cables to the surface effectively merges signals from

primarily unscattered or only slightly scattered

photons. F1His the fraction of hit OMs with ex-

actly one hit, divided by NCH. A faint signal in-

duces mostly single photoelectrons in each hit

OM and F1His close to one, while bright events

induce many photoelectrons per OM and therefore

more afterpulses, both effects resulting in F1Hclo-

ser to zero. This variable is therefore effective in

selecting bright events.

Fig. 4(right) shows F1H

for experimental data and simulated signal and

background. The air shower simulations describe

the experimental data and the simulated signal

events populate lower values of F1H. The mean

amplitude per hit OM, MA, is the sum of ampli-

tudes in hit OMs divided by NCH. Bright events

have, on average, a higher mean amplitude. The

first guess reconstruction (FG) and likelihood

reconstruction (LR) return directional informa-

tion. The quality of the likelihood reconstruction

is reflected in the likelihood

. The underlying

model for the likelihood reconstruction is a mini-

1. NCHNumber of hit OMs

2. NHITS Number of hits for all OMs

3. F1HFraction of hit OMs with exactly

one hit

4. MA Mean amplitude for hit OMs

(FG) Zenith angle obtained from

first guess

(LR) Zenith angle obtained from

likelihood reconstruction

Likelihood for likelihood

reconstruction

Smallest moment of tensor of inertia

344

M. Ackermann et al. / Astroparticle Physics 22 (2005) 339–353

mal ionizing muon that induces a comparatively

small amount of Cherenkov light in the detector

medium, while the first guess assumes light travel-

ing at a certain speed along a line

. At high ener-

gies each OM receives hundreds to thousands of

photons, significantly altering the arrival time

probability as a function of distance. This leads

to a poor resolution in the directional reconstruc-

tion for UHE events. Using the tensor of inertia

for the events, the different shapes of the air

shower and UHE neutrino induced events can be

used. From the available variables the smallest

eigenvalue of the tensor of inertia

shows the best

discrimination power.

4.2. Level 1

Selecting events with F1H< 0.65 defines the Le-

vel 1 in this analysis. The experimental data sam-

ple is reduced to 263,000 events, or 6.5% of the

initial sample. These events are reconstructed with

the first guess and the likelihood reconstruction.

The reconstructed zenith angles (

(FG),

(LR)),

the likelihood parameter

and the F1Hvariable

are used in the neural net NN1 to distinguish sim-

ulated signal from background. The simulation of

air shower events gives reasonable agreement in

the zenith angle distribution, for both first guess

and likelihood reconstructions (Fig. 5). The distri-

butions show that the reconstructions are not able

to resolve the directional information of the UHE

neutrino induced events, which are predominantly

horizontal. Nevertheless, the direction of air

shower muon events is better reconstructed and

this is exploited by the neural net NN1.

Fig. 6

shows the neural net output for experimental data,

signal Monte Carlo and the two sets of air shower

simulations. Both samples, the standard set of

CORSIKA generated data with a limited amount

of events (the outlier at NN1

0.95 corresponds

to one event) and the re-weighted high energy

CORSIKA sample using only proton and iron cos-

mic ray primaries, show good agreement with the

experimental data.

4.3. Level 2

Reducing the Monte-Carlo background to

approximately 1% of the previous level, Level 2 is

defined by selecting events with NN1 > 0.37. The

experimental data set is reduced to 3326 events,

while the air shower simulation predicts 2976 ± 51

events. This is 11% lower and within the systematic

Fig. 4. The NHITS distributions for the experiment, air shower and signal simulation to the left and to the right F1H. At F1H = 0.65

the position of the selection criteria leading to the next level is shown.

For more details on the reconstruction methods used in

AMANDA see [20].

M. Ackermann et al. / Astroparticle Physics 22 (2005) 339–353

345

uncertainty, as discussed later. At this level, the fi-

nal selection criterion is defined, based on a second

neural net (NN2) using the variables F1H, NCH,

NHITS, MA and

. Other variables and combina-

tions have been investigated, but the ones used are

found to be the most effective.

Fig. 7

shows the

NN2 output for the experiment, the air shower

and the combined electron–, muon– and tau–neu-

trino simulation. A Kolmogorov test, using the

CORSIKA generated events and the experimental

data yields a probability close to one for both cases

resulting from the same parent distribution.

Fig. 5. The zenith angle distribution for the first guess (FG) (left) and the likelihood reconstruction (LR) (right).

Fig. 6. The normalized neural net (NN1) output for the two

sets of cosmic ray air shower simulation (weighted as dotted

crosses, unweighted as triangles), the experiment and the UHE

neutrino induced events.

Fig. 7. The experimental data and the prediction from the air

shower simulation for the neural net NN2. The number of

events expected from an 10

GeVcm

neutrino

source (all flavors equally mixed) is superimposed.

346

M. Ackermann et al. / Astroparticle Physics 22 (2005) 339–353

4.4. The final selection criterion and sensitivity

The final selection criterion is based on the out-

put of the neural net NN2. To find the criterion

that puts the strongest constraint on a given theo-

retical model the procedure outlined by Hill and

Rawlins [21] is used. This method uses only infor-

mation from Monte-Carlo simulations and is

therefore free from bias introduced by using exper-

imental data. The simulated background expecta-

tion

as a function of the selection variable is

used to calculate the average event upper limit

(90% confidence limit) as defined in [22]. The

strongest constraint on a theoretical model corre-

sponds to the selection criterion that minimizes

the model rejection factor

where

is the

number of events expected from this model that

satisfy the selection criteria. The average flux

upper limit, or sensitivity, is defined as

, where

is the neutrino flux predicted by a

specific theoretical model. The model rejection fac-

tor states how strongly, on average, a given flux

is rejected when performing repeated (hypotheti-

cal) runs of the experiment. The actual experiment

will obtain a limit based on the observed number

of events. Fig. 8 shows the model rejection factor

for an

=10

GeVcm

neutrino flux.

As the neural net assigns signal-like events values

close to one, it is expected that the largest rejection

power is achieved for a selection close to this

value. Indeed, the inset inFig. 8, using finer bin-

ning, shows a minimum close to NN2 = 1. Here

NN2 > 0.9 is chosen, ignoring the loss of approxi-

mately 10% in rejection power compared to the ac-

tual minimum. For this selection,

= 7.44 ± 0.14

and

= 4.6 ± 1.2 is expected from simulations

for signal and background, respectively. This re-

sults in a sensitivity of 5.1 events (90% confidence

level), or

Þ¼

GeVcm

. At this level, by calculating

the number of equivalent events, the biased Monte

Carlo background simulation corresponds to

approximately 3 times the experimental live time.

4.5. Effective detector area

The effective area for neutrinos,

eff

, represents

the area of an ideal detector capable of detecting

neutrinos with full efficiency. Using the effective

area for neutrinos one can calculate neutrino in-

duced event rates for a given neutrino flux. The

number of events is calculated by:

event

eff

With

the live time of the experiment,

and

denote the energy and the zenith angle of the

neutrino.

Fig. 9(left) shows the effective area for

neutrinos as a function of energy for the three fla-

vors averaged over the azimuth and zenith angles.

As the energy increases the muon–neutrino contri-

bution dominates over those from electron– and

tau–neutrinos, because of the increasing path

length of the muons. At 10

GeV the detector is

approximately 4–5 times more sensitive for

muon–neutrinos than for electron–neutrinos, the

sensitivity for tau–neutrinos being in-between.

Due to the angular averaging, this figure implicitly

averages the effects of absorption and interaction

probability.

Fig. 9(right) shows that for nearly

Fig. 8. The model rejection factor for an

GeVcm

neutrino flux. The

-axis denotes the

selection with NN2 larger than the corresponding value.

Selecting events with NN2 > 0.9 leads to a model rejection

factor of 0.69.

M. Ackermann et al. / Astroparticle Physics 22 (2005) 339–353

347

horizontal events, the detection area is much larger

than the averaged area and exceeds 10

for hori-

zontal muon–neutrinos.

4.6. Event rates

The overall absolute sensitivity of the simulation

is verified by comparing the predicted event rate

from background simulations with the experimen-

tal rate. Table 2 shows the event rates for the differ-

ent selection criteria. The number of experimental

events drops from 4

to 5 and the simulated

background rate describes the experimental rate

at all levels within the systematic uncertainties.

5. Systematic uncertainties

Systematic uncertainties in simulation input

parameters lead to an uncertainty in the final re-

sult. Changes in these parameters influence the

number of expected signal or background events

for a fixed set of selection criteria. In this analysis

the main uncertainties are related to the properties

of the ice as medium for photon propagation, the

muon propagation in the ice, the absolute detector

sensitivity, the neutrino cross section at high ener-

gies and the absolute flux and composition of the

primary cosmic rays. The effects of variations in

the simulation input parameters on the number

of events remaining after the final selection are

studied. The derived systematic uncertainties are

included in the limit calculation using the method

of Conrad et al. [23], which is an extension of the

approach of Cousins and Highland [24].

5.1. Absolute detector sensitivity

There are three main uncertainties affecting the

absolute sensitivity of the detector: the absolute

Table 2

Event rates (Hz) for the different analysis levels for the experiment and the background simulation performed with CORSIKA

Selection criteria

NCH> 95 F1H< 0.65 NN1 > 0.37 NN2 > 0.9

Experiment 0.35 0.023 2.9

4.4

CORSIKA 0.31 0.026 2.6

4.1

Fig. 9. The effective area for neutrinos of all three flavors averaged over all angles (left) and for nearly horizontal events (right).

348

M. Ackermann et al. / Astroparticle Physics 22 (2005) 339–353

sensitivity of the OMs, the shadowing of the

OMs by the string-cable, and the effect of the ex-

act optical properties of the re-frozen ice enclos-

ing the OMs in the 60cm wide drill hole. The

determination of the uncertainty in the absolute

sensitivity of the OM cannot easily be decoupled

from the uncertainty in the ice properties. Fol-

lowing the discussion in

[25]

the uncertainty in

the absolute sensitivity of the OM is estimated

to be 15%.

5.2. Optical ice parameters

High energy muons generate a large number of

photons in the ice. These photons are scattered

and absorbed. Due to the large number of pho-

tons, some photons can be detected over long dis-

tances in the ice. This analysis uses an average

effective scattering and absorption length (

eff

24m,

abs

= 130m) to describe the propagation of

photons. The error on both parameters is esti-

mated to be about 10%. The parameters are not

independent, i.e. a larger scattering length implies

a larger absorption length. To estimate the system-

atic effect, we simulate the muon–neutrino signal

with (

eff

=19m,

abs

= 90m), (

eff

=22m,

abs

110m) and (

eff

=26m,

abs

= 145m) in addition

to the standard combination. The variation of

the parameters span a wider range than allowed

by the estimated uncertainty, to account for an

overall shift seen in these values when comparing

earlier[1]and newer analyses[26]of experimental

data. The variation of the ice parameters changes

the absolute number of events predicted by the

simulation. If the number of events predicted by

the simulation were to differ from the number of

observed events by significantly more than allowed

by the overall error one would introduce a normal-

ization procedure. This is taken into account when

determining the systematic uncertainty due to var-

iation of the optical parameters, by normalizing

the number of events in the leftmost (most back-

ground like) bin in the NN2 distribution arbi-

trarily to 100. UsingTable 3, the relative error of

the average number of events, 34%, is taken as sys-

tematic uncertainty introduced by the uncertainty

in the description of the optical properties of the

ice.

5.3. Muon propagation

The path length and energy loss distribution for

muons during their passage through ice is subject

to uncertainties. To investigate this effect, muons

caused by UHE neutrinos are propagated with

two different muon propagation codes [19,18]

and the number of signal events passing the final

selection NN2 > 0.9 are counted. From this, the

uncertainty related to muon propagation simula-

tion is estimated to be 6%.

5.4. Neutrino cross section

In[27]neutrino cross sections are calculated up

to 10

eV. Below 10

eV all standard sets of par-

ton distributions yield very similar cross sections.

Above this energy, the cross sections are sensitive

to assumptions made about the behavior for

0. The authors of [27] conclude that at

eV the uncertainty reaches a factor of 2. Here

the charged-current cross section is multiplied/di-

vided by a factor that increases linearly to 2 with

the energy increasing from 10

eV to 10

eV.

Again, the number of signal events passing the

final selection NN2 > 0.9 is counted and an un-

certainty of 8% is derived.

5.5. Primary cosmic ray flux

The uncertainty in the absolute primary cosmic

ray flux enters as a scaling factor for the number

of events expected from atmospheric air shower

Table 3

Number of events passing the final selection criterion

NN2 > 0.9 for different combinations of effective scattering

and absorption length

Ice model Events passing NN2 > 0.9

eff

=19m,

abs

= 90m 22.2

eff

=22m,

abs

= 110m 26.7

eff

=24m,

abs

= 130m 22.7

eff

=26m,

abs

= 145m 42.7

Average 28.6 ± 9.6

Relative error 34%

The relative difference in event numbers is an estimate of the

systematic error introduced by uncertainties in the description

of the optical ice properties.

M. Ackermann et al. / Astroparticle Physics 22 (2005) 339–353

349

simulations. Ref.

[28]

summarizes the integrated

flux averaged for different experiments and gives

the spread between the data from different experi-

ments as error. In the energy range of interest the

error on the absolute flux does not exceed 20%.

Different elements of the same energy as primary

cosmic ray particles lead to a different shower

development and can affect the number of events

expected from these air showers. The model used

for the primary cosmic ray composition taken

from

[17]

is shown in

Fig. 3. This model fits a

‘‘heavy’’ composition for high energy primaries.

Using data from the combined SPASE-AMAN-

DA experiment, a similar trend to heavier prima-

ries at higher energies is seen [29]. To investigate

the sensitivity of the analysis to the composition

of the primary cosmic rays, the proton and iron

content was varied between 0% and 100%. The

two extremes, protons only or iron only, together

with the model from Fig. 3 are shown at Level 2

Fig. 10. The shape of the distribution is not

influenced by the primary composition. After nor-

malizing to the number of events in experimental

data (3326 events), the variation in the number

of events passing the NN2 > 0.9 selection while

varying the proton/iron content is used to deter-

mine the uncertainty. Allowing the two extremes

(proton or iron only) this uncertainty is about

25%. This is an overestimation, as the proton or

iron only compositions are contradicted by other

experiments. Allowing a minimum of 20% of pro-

tons or iron as extremes decreases the uncertainty

to about 15%, the value used in this analysis.

5.6. Summary of systematic uncertainties

This analysis accounts for the major sources of

systematic uncertainties, including uncertainties in

the background simulation. The variation of the

optical properties leads to the largest error of

34%, the absolute sensitivity of the OM contrib-

utes 15%, the neutrino cross section 8% and the

muon propagation 6%. Treating these errors as

independent and adding them quadratically, the

signal uncertainty becomes 39%. For down-going

atmospheric air showers (i.e. background), we

add in quadrature the statistical uncertainty of

26% (4.6 ± 1.2 expected events), uncertainties from

composition of 15% and normalization of the

absolute flux of 20% yielding a total uncertainty

of 36%.

6. Neutrino flux limits

Fig. 7

shows the distribution of NN2 for

experimental data, the simulated air showers,

and a neutrino flux simulation with

GeVcm

. Applying the selection cri-

terion NN2 > 0.9, the simulation gives a back-

ground expectation of 4.6 ± 1.2 events while the

experiment yields 5 events for a live time of 131

days. Using the tables by Feldman and Cousins

[22] and disregarding systematic uncertainties, this

results in an upper limit of 4.7 events at 90% con-

fidence level. With this, an all flavor neutrino

source with a spectrum proportional to

limited by

= 0.63

GeVcm

Including the systematic uncertainties as evaluated

above and following the method described in [23],

the event upper limit increases to 7.35 (90% confi-

Fig. 10. NN2 for cosmic ray air shower simulations and

different primary compositions at Level 2. The composition

from [17] is also shown in Fig. 3, the other two represent the

extreme cases of only proton or iron primaries. The total

number of events is normalized to the experimental number of

events.

350

M. Ackermann et al. / Astroparticle Physics 22 (2005) 339–353

dence level) and the upper flux limit to

0.99

GeVcm

. This is 57% above

the limit without systematic uncertainties. Fig. 11

shows the energy distribution for a diffuse neutrino

flux corresponding to the above limit. Ninety per-

cent of the events are contained in the energy re-

gion from 10

eV to 3

eV, with peaks just

above 10

eV for the muon–neutrino contribution

and at the Glashow resonance (6.3PeV) for the

electron–neutrino contribution.

The experimental data can be used to set limits

on neutrino flux predictions other than a generic

spectrum. Several AGN models in the litera-

ture predict fluxes that might be detectable with

the sensitivity derived above. The pioneering

AGN core model by Stecker et al. (S91) [30] has

been updated by the more recent model (S96)

[31]. Others are the AGN jet model by Protheroe

(P97) [32] and a model by Mannheim (M95) [33].

With systematic uncertainties included, this analy-

sis excludes at 90% confidence level the neutrino

fluxes predicted by the models S91, S96 and P97

with model rejection factors between 0.24 and

0.97, while M95 is not quite excluded (see

Table

4). Other models generally predict lower fluxes,

while neutrinos from cosmic ray interactions with

Fig. 11. Energy distribution for the sum and the individual con-

tributions of the three neutrino flavors for a diffuse

neutrino flux with a strength of

= 0.99

GeVcm

after the final selection criterion. The num-

ber of events from

and

are 2.2, 3.6 and 1.5.

Table 4

Number of events expected (

) for 131 days after applying the

selection NN2 > 0.9 for a generic

source and four different

predicted AGN models (references given in the text)

Model

NN2 > 0.9

mrf mrf excl.

sys.

mrf incl.

sys.

7.44 ± 0.14 0.69 0.63 0.99

S91 7.56 ± 0.25 0.67 0.62 0.97

S96 30.5 ± 1.0 0.17 0.15 0.24

P97 13.45 ± 0.21 0.38 0.35 0.55

M95 6.17 ± 0.04 0.83 0.76 1.19

UL – 5.1 4.7 7.35

The model rejection factor is the factor by which the source

strength needs to be multiplied to equal the event upper limit

(UL). The middle column

mrf

gives the sensitivity, while the

last two columns give the experimental results for the model

rejection factor excluding and including systematic uncertain-

ties. A rejection factor <1 indicates an exclusion of the neutrino

flux caused by the model at 90% confidence level.

Fig. 12. Three models of AGN neutrino emission, S91 [30], S96

[31] and P97 [32] which are excluded by this analysis and the not

quite excluded model M95

[33]

are shown as well as the

experimental 90% confidence level upper limit to an diffuse

all flavor neutrino flux as a bold solid line. The dotted line

shows the sensitivity of this analysis. The thin line to the left

shows the AMANDA-II all flavor limit [35] for lower energies.

The range of the presented limit corresponds to the region that

contains 90% of the expected signal.

M. Ackermann et al. / Astroparticle Physics 22 (2005) 339–353

351

the microwave background or from decays of

topological defects are too high in energy and

too low in flux for the achieved sensitivity.

7. Summary and discussion

Data recorded with the AMANDA-B10 detec-

tor in 1997 are searched for leptons caused by a

diffuse flux of UHE neutrinos. In contrast to the

analyses [26] and [34] which used the AMANDA

detector to search for an upward traveling flux of

neutrinos, or the analysis

[35]

which optimized

for cascades at lower energies, this analysis

searches for a UHE signal from horizontal and

down-going events. Restricting the analysis to very

bright events, the flux of down-going muons

caused by atmospheric air showers can be suffi-

ciently suppressed while retaining a large sensitiv-

ity to neutrinos. At all levels, the experimental

data are described well by the air shower simula-

tion. The sensitivity (excluding systematic errors)

of this analysis to an equally mixed all flavor neu-

trino flux is

GeVcm

Including a combined error (statistical and system-

atic) of 36% for the background and 39% for the

signal simulation, this analysis sets a flux upper

limit for 131 days of

(

= 1:1:1) =

0.99

GeVcm

at 90% confidence

level, shown as bold line in

Fig. 12. The energy

range 10

–3

eV contains 90% of the neu-

trino induced events, with the remainder being

equally divided above and below this range. This

energy range is well suited to exploring neutrino

emission models from AGN blazars, and three

specific model predictions, two by Stecker et al.

[30,31]

and one by Protheroe

[32], are excluded.

The recent analysis [35] has excluded the two mod-

els by Stecker et al., but not the model by Prothe-

roe. An extension to even higher energies would be

desirable in order to explore neutrino emission

from the decay of topological defects or to search

for the guaranteed UHE neutrinos from interac-

tions of the highest energy cosmic rays with the

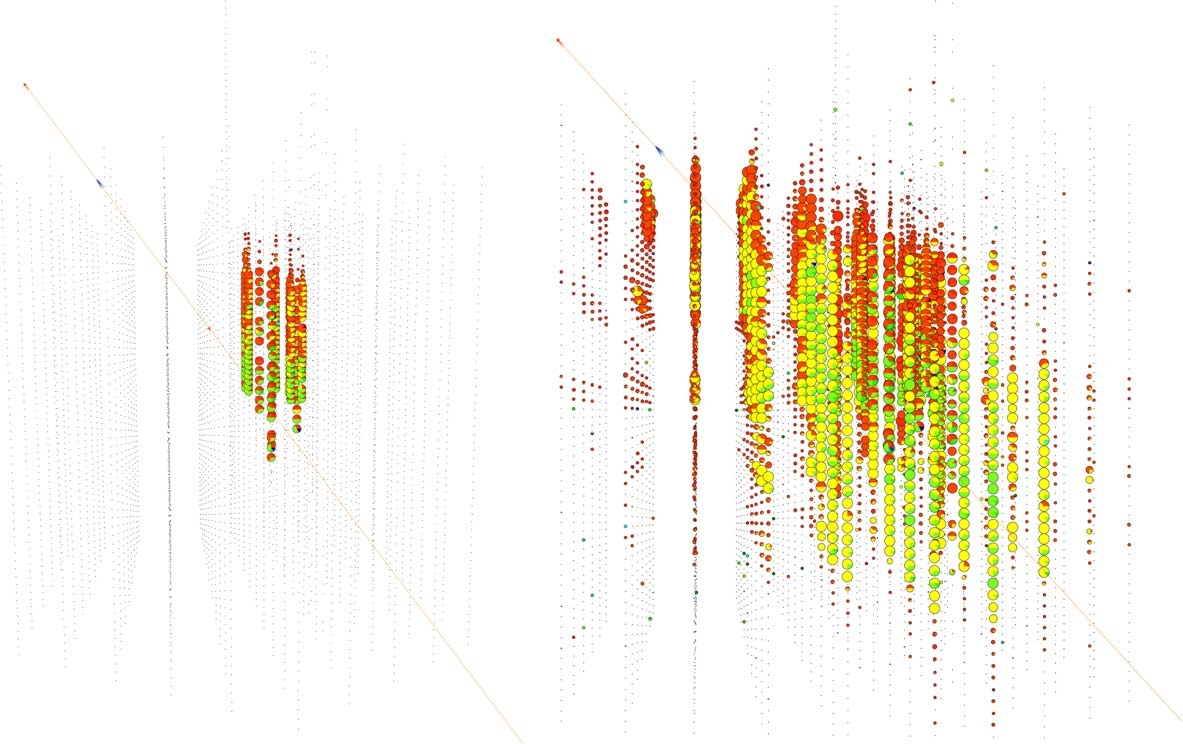
Fig. 13. The same UHE muon–neutrino event in the AMANDA-B10 detector (left) and the IceCube array (right), illustrating the

amount of additional information gained by the larger size of the detector and the larger number of optical modules in IceCube.

352

M. Ackermann et al. / Astroparticle Physics 22 (2005) 339–353

microwave background radiation. This is pre-

vented by the limited size and relatively small

number of OMs of the AMANDA-B10 detector,

where saturation effects become visible. However

the larger AMANDA-II detector

[36]

equipped

with optical fibers for dispersion free signal trans-

mission and its advanced technique of waveform

capture will improve the analysis of UHE neutri-

nos, as will the IceCube detector [37] on a longer

time scale.

Fig. 13

shows the simulated response

to a muon caused by an UHE neutrino interaction

passing the AMANDA-B10 and IceCube array,

respectively. In particular the IceCube array, with

construction beginning during 2004/2005, will dra-

matically increase the amount of information

exploitable in the UHE regime.

Acknowledgements

We acknowledge the support of the following

agencies: National Science Foundation––Office of

Polar Programs, National Science Foundation––

Physics Division, University of Wisconsin Alumni

Research Foundation, Department of Energy and

National Energy Research Scientific Computing

Center (supported by the Office of Energy Re-

search of the Department of Energy), UC-Irvine

ANEAS Supercomputer Facility, USA; Swedish

Research Council, Swedish Polar Research Secre-

tariat and Knut and Alice Wallenberg Founda-

tion, Sweden; German Ministry for Education

and Research, Deutsche Forschungsgemeinschaft

(DFG), Germany; Fund for Scientific Research

(FNRS-FWO), Flanderns Institute to encourage

Scientific and Technological Research in Industry

(IWT) and Belgian Federal Office for Scientific,

Technical and Cultural affairs (OSTC), Belgium;

Fundacio

n Venezolana de Promocio

n al Investig-

ador (FVPI), Venezuela; D.F.C acknowledges the

support of the NSF Career program; E.R.

acknowledges the support of the Marie-Currie fel-

lowship program of the European Union.

References

[1] E. Andres et al. [AMANDA Collaboration], Nature 410

(2001) 441.

[2] R. Gandhi et al., Phys. Rev. D 58 (1998) 093009.

[3] J.R. Klein, A.K. Mann, Astropart. Phys. 10 (1999) 321.

[4] S. Hundertmark et al. [AMANDA Collaboration], Proc.

27th Int. Cosmic Ray Conf., Hamburg, Germany (2001)

1129.

[5] E. Waxman, Nucl. Phys. Proc. Suppl. 100 (2001) 314.

[6] J.G. Learned, K. Mannheim, Ann. Rev. Nucl. Part. Sci. 50

(2000) 679.

[7] R.J. Protheroe, arXiv:astro-ph/9612213.

[8] H. Athar et al., Phys. Rev. D 62 (2000) 103007.

[9] L. Anchordoqui et al., arXiv:hep-ph/0407020.

[10] S. Hundertmark et al. [AMANDA Collaboration], DESY-

PROC-2002-01, 2002, 69.

[11] Photonis, Photomultiplier tubes,

http://www.photonis.

com.

[12] Hamamatsu, Photomultiplier Tubes, Basics and Applica-

tions, second ed., 1999.

[13] M. Kowalski and A. Gazizov, arXiv:astro-ph/0312202.

[14] A.M. Dziewonski, D.L. Anderson, Phys. Earth Planet.

Interiors 25 (1981) 297.

[15] D. Heck, DESY-PROC-1999-01 (1999) 227.

[16] B. Wiebel-Sooth, P. Biermann, Landolt-Bornstein, vol. VI/

3c, Springer Verlag, 1999, pp. 37–90.

[17] R. Glasstetter et al. [KASCADE Collaboration], FZKA-

6345E (1999).

[18] D. Chirkin, W. Rhode, arXiv:hep-ph/0407075.

[19] P. Lipari, T. Stanev, Phys. Rev. D 44 (1991) 3543.

[20] J. Ahrens et al. [AMANDA Collaboration], Nucl.

Instrum. Methods A 524 (2004) 169.

[21] G.C. Hill, K. Rawlins, Astropart. Phys. 19 (2003) 393.

[22] G.J. Feldman, R.D. Cousins, Phys. Rev. D 57 (1998)

3873.

[23] J. Conrad et al., Phys. Rev. D 67 (2003) 012002.

[24] R.D. Cousins, V.L. Highland, Nucl. Instrum. Methods A

320 (1992) 331.

[25] J. Ahrens et al. [AMANDA Collaboration], Astrophys. J.

583 (2003) 1040.

[26] J. Ahrens et al. [AMANDA Collaboration], Phys. Rev.

Lett. 90 (2003) 251101.

[27] R. Gandhi et al., Astropart. Phys. 5 (1996) 81.

[28] J.R. Hoerandel, Astropart. Phys. 19 (2003) 193.

[29] T. Miller et al. [SPASE and AMANDA Collaborations],

Astropart. Phys. 21 (2004) 565.

[30] F.W. Stecker et al., Phys. Rev. Lett. 66 (1991) 2697;

F.W. Stecker et al., Phys. Rev. Lett. 69 (1992) 2738

(Erratum).

[31] F.W. Stecker, M.H. Salamon, Space Sci. Rev. 75 (1996)

341.

[32] R.J. Protheroe, arXiv:astro-ph/9607165.

[33] K. Mannheim, Astropart. Phys. 3 (1995) 295.

[34] J. Ahrens et al. [AMANDA Collaboration], Phys. Rev. D

67 (2003) 012003.

[35] M. Ackermann et al. [AMANDA Collaboration], Astro-

part. Phys. 22 (2004) 127.

[36] S.W. Barwick et al. [AMANDA Collaboration], arXiv:

astro-ph/0211269.

[37] IceCube Project web page, http://icecube.wisc.edu.

M. Ackermann et al. / Astroparticle Physics 22 (2005) 339–353

353