doi:10.1016/j.astropartphys.2004.04.007

Measurement of the cosmic ray composition at the knee

with the SPASE-2/AMANDA-B10 detectors

AMANDA and SPASE Collaborations

J. Ahrens

, M. Ackermann

, E. Andres

, X. Bai

d,1

, S.W. Barwick

R.C.Bay

,T.Becka

,K.-H.Becker

,E.Bernardini

,D.Bertrand

,F.Binon

A. Biron

, D.J. Boersma

,S.B

€

oser

, O. Botner

, A. Bouchta

, O. Bouhali

T. Burgess

, S. Carius

, T. Castermans

, D. Chirkin

, J. Conrad

, J. Cooley

D.F. Cowen

, A. Davour

, C. De Clercq

, T. DeYoung

c,2

, P. Desiati

J.-P. Dewulf

, E. Dickinson

n,1

, P. Ekstr

€

, R. Engel

d,3

, P. Evenson

d,1

T. Feser

, T.K. Gaisser

d,1

, R. Ganugapati

, M. Gaug

, H. Geenen

L. Gerhardt

, A. Goldschmidt

, A. Hallgren

, F. Halzen

, K. Hanson

R. Hardtke

, T. Hauschildt

, M. Hellwig

, P. Herquet

, G.C. Hill

J.A. Hinton

n,1

, D. Hubert

, B. Hughey

, P.O. Hulth

, K. Hultqvist

S.Hundertmark

,J.Jacobsen

,A.Karle

,J.Kim

,L.K

€

opke

,M.Kowalski

K. Kuehn

, J.I. Lamoureux

, H. Leich

, M. Leuthold

, P. Lindahl

I. Liubarsky

, J. Lloyd-Evans

n,1

, J. Madsen

, K. Mandli

, P. Marciniewski

H.S. Matis

, C.P. McParland

, T. Messarius

, T.C. Miller

d,4

, Y. Minaeva

P. Mio

cinovi

f,5

, P.C. Mock

e,6

, R. Morse

, R. Nahnhauer

, T. Neunh

€

offer

P. Niessen

, D.R. Nygren

,H.

€

Ogelman

, Ph. Olbrechts

C.P

erezdelosHeros

,A.C.Pohl

,R.Porrata

e,7

,P.B.Price

,G.T.Przybylski

K. Rawlins

, E. Resconi

, W. Rhode

, M. Ribordy

, S. Richter

K.Rochester

n,1

,J.Rodr

ıguezMartino

,D.Ross

,H.-G.Sander

,T.Schmidt

K. Schinarakis

, S. Schlenstedt

, D. Schneider

, R. Schwarz

, A. Silvestri

M. Solarz

, G.M. Spiczak

r,1

, C. Spiering

, M. Stamatikos

, T. Stanev

d,1

Corresponding author. Fax: +1-949-824-2174.

E-mail address:

sbarwick@uci.edu(S.W. Barwick).

SPASE Collaboration.

Department of Physics, University of Maryland, College Park, MD 20742.

Present address: Forschungszentrum Karlsruhe, Institut fur Kernphysik, Postfach 3640, 76021 Karlsruhe, Germany.

Present address: Applied Physics Laboratory, Johns Hopkins University, Laurel, MD 20723, USA.

Department of Physics and Astronomy, University of Hawaii, Honolulu, HI 96822, USA.

Present address: SEA Inc. 7545 Metropolitan Dr. San Diego, CA 92108, USA.

Present address: L-174, Lawrence Livermore National Laboratory, 7000 East Ave., Livermore, CA 94550, USA.

0927-6505/$ - see front matter

doi:10.1016/j.astropartphys.2004.04.007

Astroparticle Physics 21 (2004) 565–581

www.elsevier.com/locate/astropart

D. Steele

, P. Steffen

, R.G. Stokstad

, K.-H. Sulanke

, I. Taboada

S. Tilav

d,1

, C. Walck

, W. Wagner

, Y.-R. Wang

, A.A. Watson

n,1

C.H. Wiebusch

, C. Wiedemann

, R. Wischnewski

, H. Wissing

K. Woschnagg

,W.Wu

, G. Yodh

, S. Young

Institute of Physics, University of Mainz, Staudinger Weg 7, D-55099 Mainz, Germany

DESY-Zeuthen, D-15735 Zeuthen, Germany

Department of Physics, University of Wisconsin, Madison, WI 53706, USA

Bartol Research Institute, University of Delaware, Newark, DE 19716, USA

Department of Physics and Astronomy, University of California, Irvine, CA 92697, USA

Department of Physics, University of California, Berkeley, CA 94720, USA

Fachbereich 8 Physik, BUGH Wuppertal, D-42097 Wuppertal, Germany

Universit

Libre de Bruxelles, Science Faculty CP230, Boulevard du Triomphe, B-1050 Brussels, Belgium

Division of High Energy Physics, Uppsala University, S-75121Uppsala, Sweden

Department of Physics, Stockholm University, SCFAB, SE-10691 Stockholm, Sweden

Department of Technology, Kalmar University, S-39182 Kalmar, Sweden

Universit

de Mons-Hainaut, 19 Avenue Maistriau 7000, Mons, Belgium

Department of Physics, Pennsylvania State University, University Park, PA 16802, USA

School of Physics and Astronomy, University of Leeds, Leeds LS2 9JT, UK

Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA

Vrije Universiteit Brussel, Dienst ELEM, B-1050 Brussel, Belgium

Imperial College, London SW7 2AZ, UK

Department of Physics, University of Wisconsin, River Falls, WI 54022, USA

Departamento de Fı

sica, Universidad Simon Bolı

var, Apdo. Postal 89000, Caracas, Venezuela

Received 6 February 2004; accepted 5 April 2004

Available online 26 May 2004

Abstract

The mass composition of high-energy cosmic rays at energies above 10

eV can provide crucial information for the

understanding of their origin. Air showers were measured simultaneously with the SPASE-2 air shower array and the

AMANDA-B10 Cherenkov telescope at the South Pole. This combination has the advantage to sample almost all high-

energy shower muons and is thus a new approach to the determination of the cosmic ray composition. The change in

the cosmic ray mass composition was measured versus existing data from direct measurements at low energies. Our data

show an increase of the mean log atomic mass

by about 0.8 between 500 TeV and 5 PeV. This trend of an

increasing mass through the ‘‘knee’’ region is robust against a variety of systematic effects.

Keywords:

Cosmic Rays; Neutrino astronomy; Mass composition

1. Introduction

Cosmic rays observed at Earth follow a steep

power-law spectrum over many orders of magni-

tude in energy. At an energy of approximately

3 PeV, however, the spectral index steepens; this

feature is called the ‘‘knee’’. To understand the

reason for the knee, one must understand the

source, acceleration mechanism, and propagation

of cosmic rays. For instance, first-order Fermi

acceleration, thought to explain cosmic rays below

the knee, has a natural cutoff energy which de-

pends on the rigidity of the nucleus being accel-

erated. Observing the mass composition of cosmic

rays at the knee therefore provides an important

clue to the origin of cosmic rays.

The study of high-energy cosmic rays has led to

the construction of large ground-based air shower

566

J. Ahrens et al. / Astroparticle Physics 21 (2004) 565–581

arrays to explore the energy range above 100 TeV

where the cosmic ray flux is too low for direct

measurements. These arrays, unlike satellite- or

balloon-borne instruments, must reconstruct the

properties of primary cosmic rays indirectly, from

the behavior of the extensive air shower particles

produced in the atmosphere. The different particle

components of an air shower (electrons, photons,

muons, and hadrons) can be measured using dif-

ferent detection techniques. Since the behavior of

any one particle component generally depends on

both primary energy and primary mass, multi-

component measurements are proving to be a

powerful detection tool.

One such multicomponent experiment is

SPASE/AMANDA, a scintillator array and deep-

ice Cherenkov telescope working in coincidence at

the South Pole. SPASE measures the electron

component of the air showers at the surface, while

AMANDA measures muon bundles at depths of

1500–2000 m. By combining electron and muon

information, the primary cosmic ray energy and

mass can be estimated for each coincidence event.

2. The SPASE and AMANDA detectors

The South Pole Air Shower Experiment

(SPASE-2, or SPASE in this paper) is a scintillator

array consisting of 120 modules grouped into 30

stations on a 30 m triangular grid. The SPASE site

on the surface lies about 400 m from the center of

the AMANDA hole locations, at an atmospheric

depth of

685g cm

[1].

The Antarctic Muon And Neutrino Detector

Array (AMANDA) uses the natural ice at the

South Pole as the target and detection volume for

a large-scale Cherenkov telescope [2]. Currently,

an array of 677 optical modules (OM’s) containing

photomultipliers is frozen in the ice. This work

uses data from 1998, in which the detector com-

prised 302 OM’s on 10 strings between depths of

1500 and 2000 m. The OM’s measure the Cher-

enkov light emitted by charged particles traveling

faster than the speed of light in ice. AMANDA’s

primary mission is the detection of high-energy

neutrinos by collecting Cherenkov light emitted by

their interaction product, a lepton such as a muon.

A neutrino-induced muon is only identifiable by its

upgoing direction. Misreconstructed downgoing

cosmic ray muons (produced in the atmosphere

above the South Pole) constitute the dominant

background for neutrino-induced muons, and so

great care is taken to remove them from neutrino

analyses. In this work, however, cosmic ray muons

are the

signal

, rather than the background. Some

difficulties of the neutrino analysis can be avoided

here, while a cosmic ray analysis presents new and

different challenges of its own.

3. Shower reconstruction in SPASE

SPASE data analysis reconstructs the shower

direction from the arrival times of charged parti-

cles in the array’s scintillators. The shower core

location and shower size are reconstructed by fit-

ting the lateral distribution of particle density to

the Nishimura–Kamata–Greisen (NKG) function

[3] and then evaluating this lateral distribution at a

fixed distance from the shower core. In particular,

SPASE data analysis computes for each event the

shower parameter

(30), the measured particle

density at 30 m from the shower core, in units of

equivalent minimum ionizing vertical muons per

. The shower core can be reconstructed within a

few meters, and the shower direction to within 1.5

at low energies, improving to less than 0.4

higher energies [4].

(30) can be used as an energy

estimator, but it is not entirely composition-inde-

pendent. The shower size depends also on the

height of interaction in the atmosphere, which in

turn depends on the primary mass. A detailed

description of how

(30) is measured can be found

in references [1,5].

4. Reconstruction in AMANDA

Just as SPASE is used to reconstruct the posi-

tion, direction, and electron size of an air shower

event, a similar procedure is developed for the

analysis of the muon bundle in AMANDA. First,

the combined detectors are used to get the bundle’s

position and direction more accurately than can be

achieved using either detector alone. Then, the

J. Ahrens et al. / Astroparticle Physics 21 (2004) 565–581

567

expected lateral distribution function (LDF) of

photons from a muon bundle is computed. Two

corrections must be applied to the LDF in order to

be able to apply it to all OM’s and all depths. The

first accounts for the ranging-out of muons be-

tween the top of the detector and the bottom. The

second accounts for the changing scattering length

in the ice, due to variation of concentration of

impurities such as dust in ice. For each event, the

LDF is fitted to OM amplitudes and evaluated at a

fixed distance of 50 m from the center of the

bundle to compute a parameter called

. This

parameter is analogous to

(30) but measures

muon energy loss rather than electron density. The

technique is described in more detail below.

4.1. Track reconstruction

The standard AMANDA track reconstruction,

described in [6], is performed by the reconstruction

program recoos. To reconstruct muon direction in

normal operation, recoos varies the position

;

of a point on the track and its direction

;

, until the track hypothesis (a single muon

line source) is most likely to have given rise to the

observed light pattern. SPASE coincidences,

however, provide additional information: the

shower core location at the surface (within 3–4 m)

and shower direction (within 1.5

). A better track

can be found by fixing the track position at the

reconstructed shower core in SPASE, using SPA-

SE’s reconstructed track as a first guess, and

allowing

recoos

to vary

only

the direction angles

;

as free parameters. The long lever arm be-

tween the two detectors (about 1750 m center-

to-center) gives this technique great accuracy, less

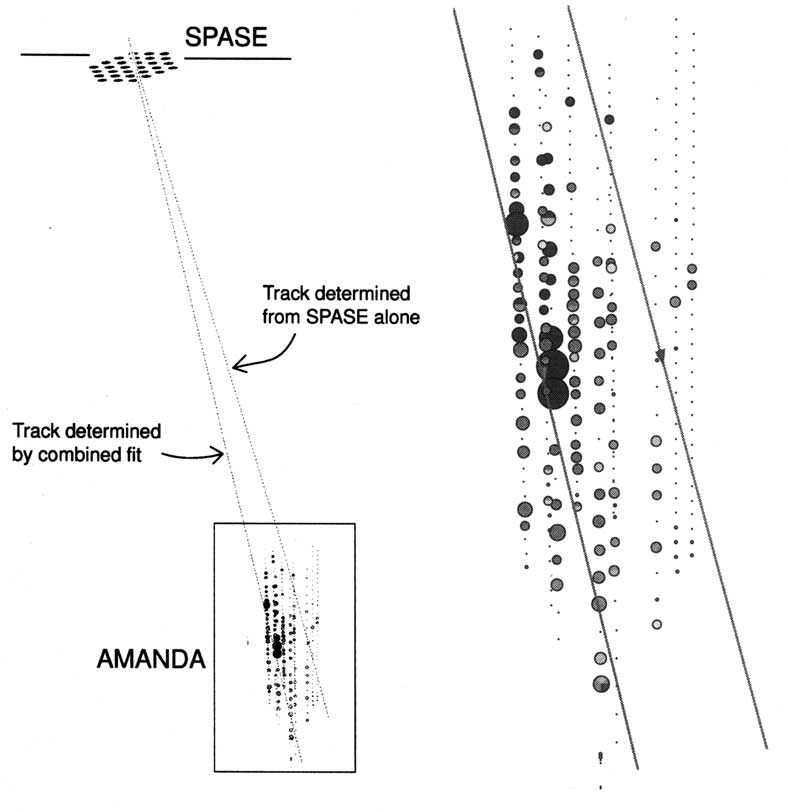
than a half degree. Fig. 1 shows the relative posi-

tions of SPASE and AMANDA, and how the

SPASE reconstruction alone can be improved by

using both detectors with this combined technique.

Fig. 1. SPASE/AMANDA coincidence event from 1997 data.

568

J. Ahrens et al. / Astroparticle Physics 21 (2004) 565–581

4.2. Muons in AMANDA

High-energy muons (meaning in this context,

muons of energy above 300 GeV which can reach

the detector at depth) are created by the decay of

high-energy charged pions and kaons originating

high in the atmosphere in the early stages of

shower development. The Gran Sasso laboratories

(housing the underground LVD and MACRO

experiments) have explored the potential of coin-

cidences between surface electrons from EAS-TOP

and TeV muons [7–10]. Due to their small size,

MACRO and similar experiments sample only a

few individual muons from the air shower.

AMANDA is shallower (resulting in a lower muon

energy threshold) and also much larger. It can also

detect light up to 150 m from the muon bundle.

AMANDA can measure the energy loss of the

muon bundle at depth, but it is too sparse an array

to resolve individual muons. This makes AMAN-

DA a fundamentally different kind of cosmic ray

detector, requiring new techniques. Therefore in

this paper we must devote some time to the physics

of muon bundles emitting light in ice, and the

introduction of a new technique for reconstructing

the total muon energy loss using photomultiplier

pulse amplitudes recorded by AMANDA.

The differential energy spectrum of the muons

in a shower at the surface follows a power law with

spectral index

)

2.757 [11]. As the muons penetrate

the ice, their energy loss can be described by [12]

eff

with values of

eff

and

eff

for ice also taken from

[12]. From the surface spectrum and this differen-

tial equation, one can calculate the distribution of

the number of muons surviving to slant depth

depth

Þ¼

surface

Þ¼

757

eff

757

This equation also describes how the muon

intensity within a single event changes as the

bundle propagates through the detector from 1500

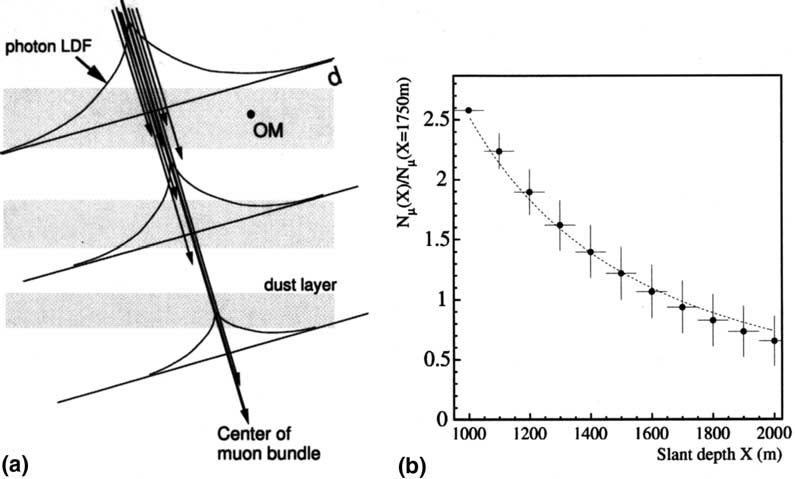
m at the top to 2000 m at the bottom, illustrated in

Fig. 2(a). Simulations of muons propagating

through these depths of ice are compared in Fig.

2(b) to this simple functional form, which will be

used later for computing the range-out correction

to the photon LDF.

Only muons with a surface energy of more than

300 GeV survive to AMANDA depth. The

transverse momentum of these muons is small

Fig. 2. Propagation of muons through the ice: (a) schematic representation of how the ranging out of muons affects the photon LDF;

(b) ratio of muons reaching slant depth

, as a function of

, averaged over many simulated events. The fraction is defined to be

relative to the arbitrary reference slant depth of 1750 m, which is the distance from the center of SPASE to the center of AMANDA.

Dashed line: Muon fraction calculated using Eq. (2) in the text.

J. Ahrens et al. / Astroparticle Physics 21 (2004) 565–581

569

compared to their longitudinal momentum, so the

muons are tightly contained in a bundle. Simula-

tions show that on average 90% of all muons

reaching the detector level are contained within a

radius of

20 m in 1 PeV proton-induced showers.

In iron-induced showers of the same energy this

radius increases to

30 m.

4.3. Light from muons in ice

At the wavelengths relevant to AMANDA,

between 300 and 600 nm, impurities (dust) are the

most important contributor to both absorption

and scattering of light in deep Antarctic ice. A

YAG laser at a wavelength of 532 nm was first

used to map the effective scattering length,

, and

the absorption length,

, as functions of depth

[13], revealing vertical fluctuations due to dusty

layers of ice. More recently,

in-situ

light emitters at

a variety of other wavelengths (470 nm with blue

LEDs, 370 nm with UV LEDs, and 337 nm with a

Nitrogen laser) [14] have confirmed the predicted

wavelength dependence of both scattering [15] and

absorption [16].

For a

line

source of light, the photon intensity

seen by an OM is the integrated contribution from

many infinitesimal length elements. At distances

large compared to

the photon intensity is de-

scribed by a modified Bessel function of the second

kind [16]:

Þ/

;

where

is the perpendicular distance from the OM

to the primary track, and

is an effective propa-

gation length due to the combined effects of

absorption and scattering, given by

ffiffiffiffiffiffiffiffiffiffiffiffiffiffi

For large enough values of its argument

, the

Bessel function

, can be approximated as

ffiffiffiffiffiffiffiffiffiffiffiffiffiffi

. The photon LDF for a particular ice

layer can then be described by:

Þ/

ffiffiffiffiffiffiffiffi

At large distances, photons have been travelling

through ice layers of different quality, which to-

gether can be described by a bulk ice propagation

length

. At near distances, the propagation

length of the OM’s local ice layer

Þ¼

ice

is more appropriate. The depth-depen-

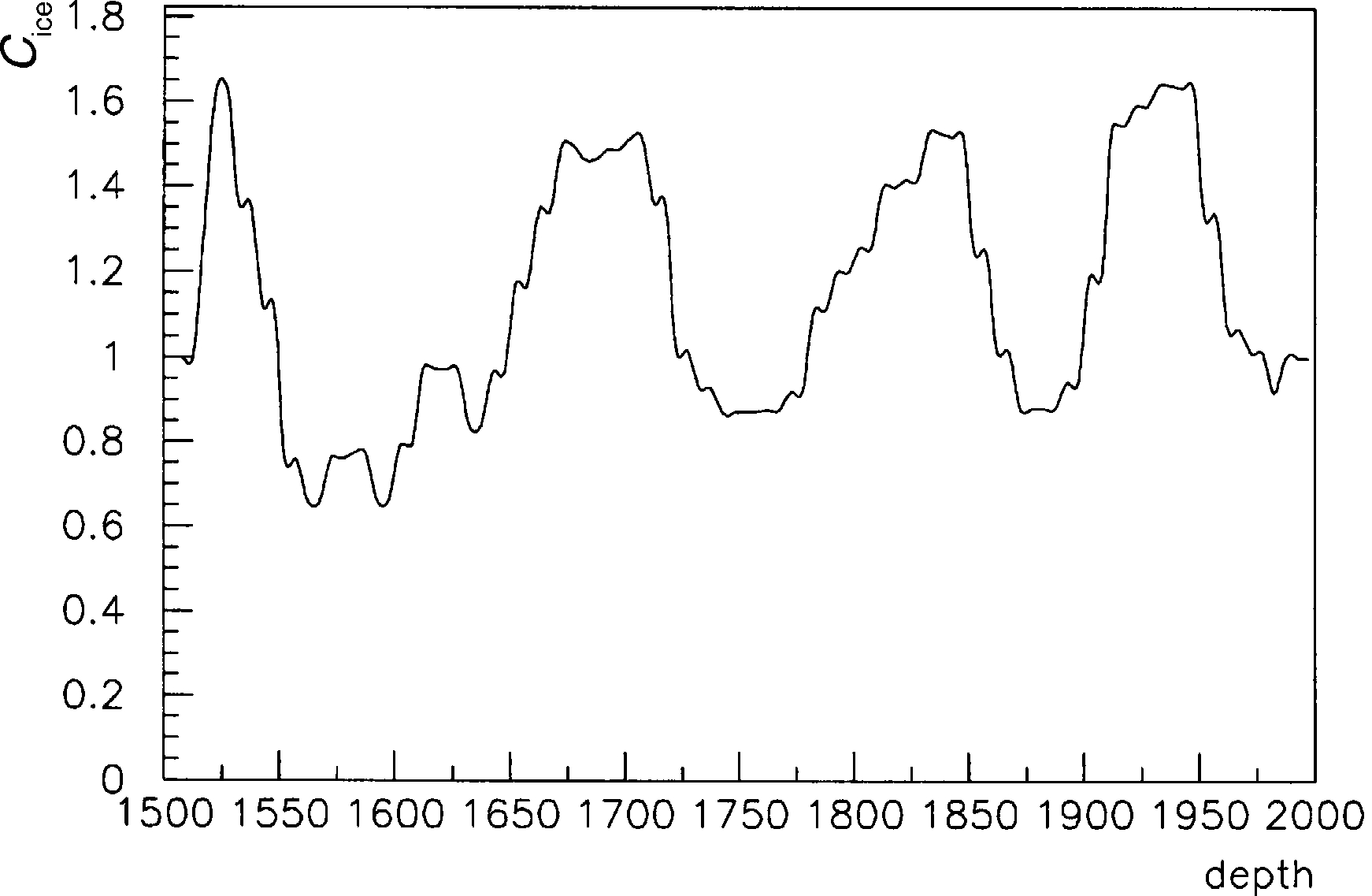
dent correction factor

ice

, shown in Fig. 3, is

taken from in-ice measurements of the variation of

scattering length around the average value [13].

For an approximate treatment of the effect of dust

layers at

all

distances, the photon LDF can be

described by a split function which employs

below a transition distance

and

above it

;

Þ/

ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi

ice

ÞÞ

;

ffiffiffiffiffiffiffi

;

This functional form fits well to data when a

value of 80 m, which is comparable to the spacing

between depths with peak concentration of dust, is

used for the transition distance

4.4. Complete LDF fit

The complete photon LDF for all depths and

distances incorporates both the range-out correc-

tion and the ice correction. An expected OM

amplitude

, follows the same functional form

and is proportional to the LDF intensity

depth

;

Þð

where the overall normalization,

, absorbs other

normalization factors and also converts the result

Fig. 3. The ice correction

ice

as a function of depth, from in-

ice scattering data.

570

J. Ahrens et al. / Astroparticle Physics 21 (2004) 565–581

into units of OM amplitude (photoelectrons).

also proportional to the total amount of light

emitted by the muon bundle.

With the track position and direction held fixed,

recoos maximizes the likelihood

of the ampli-

tudes measured by AMANDA modules to derive

from the expected functional form:

all OM

measured

;

where

is a Poisson probability. The overall

normalization

and the bulk propagation length

are left as free parameters.

is proportional to

the total energy loss of muons in the ice.

known from in-ice measurements to be about 26 m

[13]. However, errors in track reconstruction can

cause a change in the best-fit slope of the LDF. If

instead we fit

as a free parameter and then

evaluate the resulting reconstructed LDF at a fixed

distance, we can achieve a very stable measure-

ment of the overall muon energy loss. The recon-

structed

can also be used as a cut parameter to

ensure that the LDF for the fitted event has been

reconstructed sensibly.

The fit LDF is evaluated at a constant distance,

in this case 50 m; this distance offers the most

stable measurement under simultaneous variations

in fitted

and

due to errors in track recon-

struction. The parameter

50 is defined as

the value of the fit LDF function, evaluated in

the absence of correction factors (meaning

depth

Þ¼

1and

ice

Þ¼

1), and at a distance of

50 m from the primary track

ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi

50 m

?ð

50 m

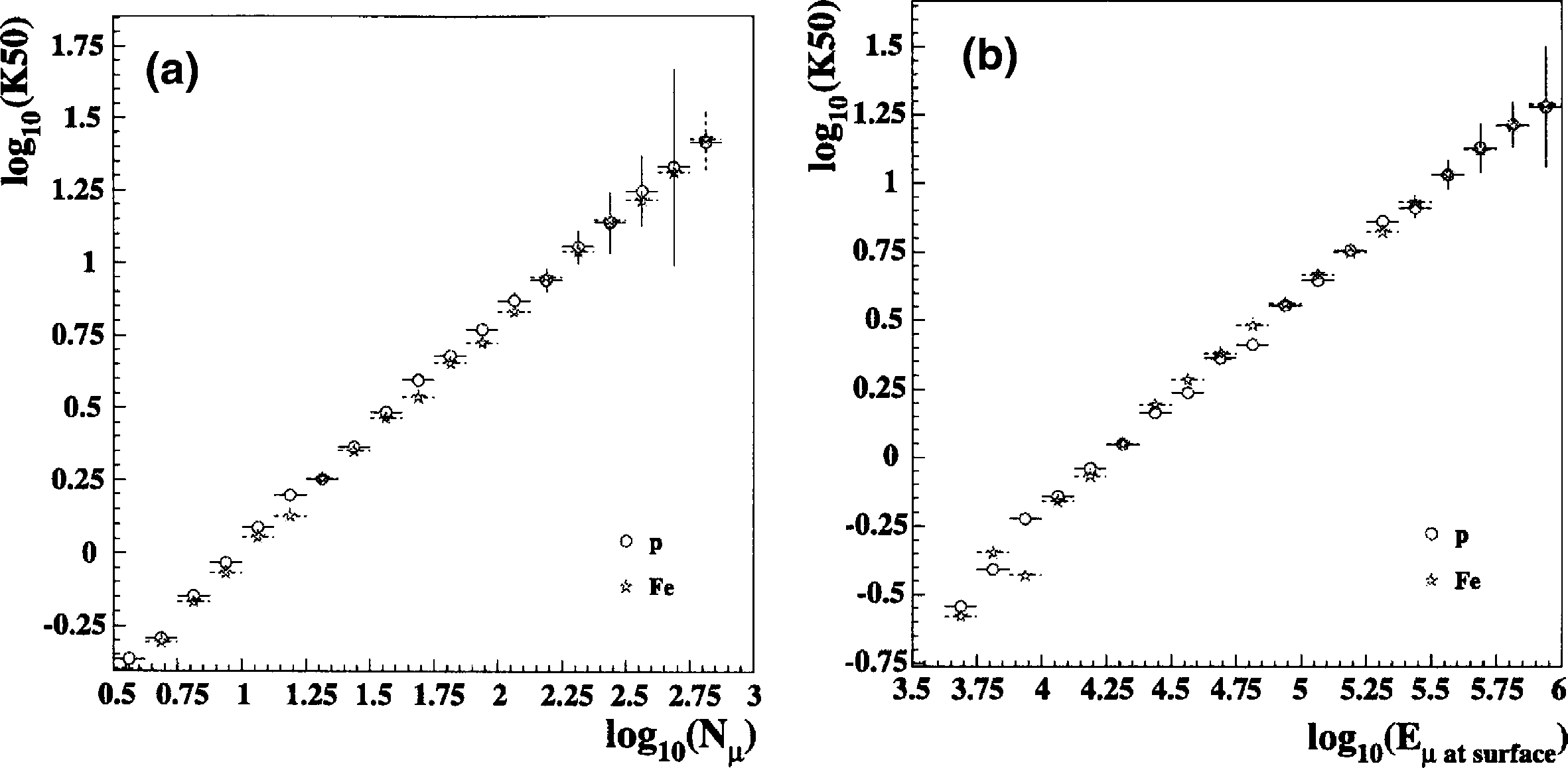
50 is analogous to similar parameters used by

other experiments, and is a measurement of muon

energy loss. This parameter is also well-correlated

with the number of muons in the bundle, shown in

Fig. 4(a), and with the total muon energy at the

surface, shown in Fig. 4(b) (see Section 5.2 for a

description of the simulation procedure). These

correlations are nearly composition-independent.

50 is not, however, a direct measurement of the

number of muons that reach the detector, since it

also accounts for the emission and propagation of

the Cherenkov light through the ice that surrounds

the AMANDA optical modules.

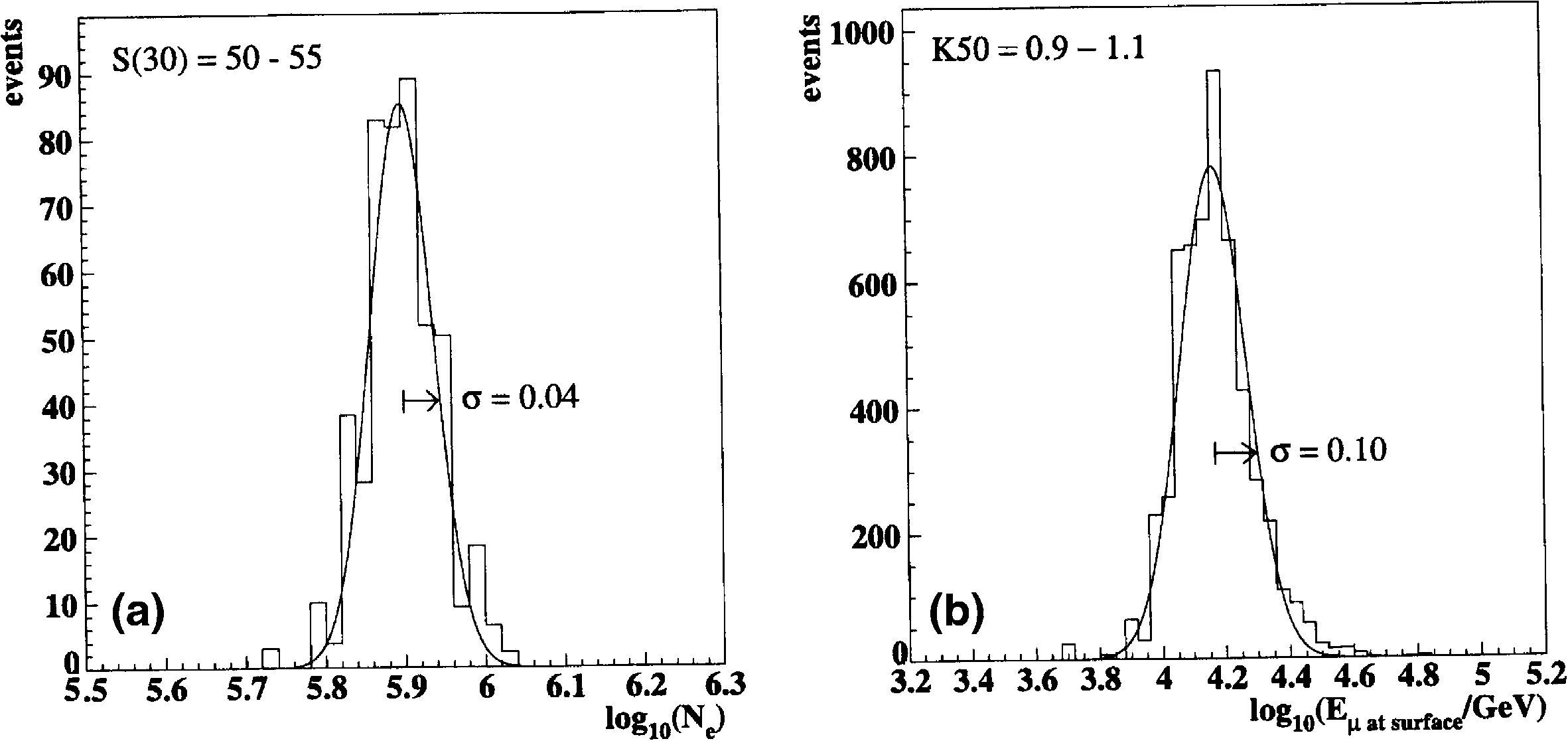
Fig. 5 shows the resolutions of the two

parameters we will use together to measure cosmic

ray energy and mass:

and

50. A measure-

ment of

in SPASE relates to the total num-

ber of electrons in the shower, with a resolution

shown in Fig. 5 (a): 0.04 in log

for

between 50 and 55 m

. A measurement of

in AMANDA relates to the total muon energy,

with a resolution shown in Fig. 5(b) 0.10 in

log

(

at surface

for

50 between 0.9 and 1.1 pho-

toelectron/OM. It may be noted that an event of

this brightness generates a total of about 300

photoelectrons summed over all OM’s.

Fig. 4. The reconstructed

50 resolution, for proton and iron simulations (the irregularity at low energies is a small-statistics fluc-

tuation): (a)

50 vs. the true number of muons at 1750 m slant depth and (b)

50 vs. the true total muon energy at the surface.

J. Ahrens et al. / Astroparticle Physics 21 (2004) 565–581

571

5. Data and Monte Carlo samples

5.1. Data

SPASE/AMANDA coincidence data from 1998

were used for the results in this work (though data

from 1997 were used first to explore the tech-

niques). AMANDA operated in slave mode to

SPASE, reading out all OM’s upon receiving an

SPASE trigger externally. Events were matched

together offline by comparing GPS times (each

detector has its own independent clock) and

requiring a match within 1 ms. A more detailed

description of how SPASE and AMANDA oper-

ate in coincidence can be found in [17]. Coinci-

dence events between SPASE and AMANDA

have zenith angles of between 8

and 18

,with

additional quality cuts confining this range even

further.

5.2. Monte Carlo simulations

The simulation used in this work employs a

modified version of the air shower code MOCCA

[18] using the QGSJET98 interaction model [19].

We simulated 350 000 proton- and iron-induced

showers according to an

spectrum from ener-

gies of 100 TeV to about 100 PeV, and from angles

of 0

to 30

. The events are re-weighted to a cosmic

ray energy spectrum, with a spectral index of

)

2.7

below a knee at 3 PeV and

)

3.0 above it. The

surface component is processed through the

SPASE detector simulation. Whenever SPASE is

triggered by the simulated air shower, the SPASE

scintillator data together with the muon informa-

tion are recorded. The high-energy muons are then

propagated through the ice with the muon prop-

agator PROPMU [20]. The Cherenkov photons

generated by the muon are finally propagated

through the ice and events are simulated with a

detailed AMANDA detector simulation. The sys-

tematic uncertainties associated with these simu-

lations will be discussed further on, together with

the results.

5.3. Quality cuts

A small set of quality cuts ensures an event

sample where both SPASE and AMANDA have

reliably reconstructed the track direction and the

parameters

and

50.

•

The shower is large enough to reconstruct size

Small showers are not well reconstructed, so an

iterative determination of

is not performed

when the first determination gave

. All events with

less than m

are dis-

carded in this analysis at an early stage.

•

The track passes within the AMANDA array

SPASE tracks which pass

outside

AMANDA

tend to get pulled

by the combined track fit

described in Section 4.1. Thus, we require the

Fig. 5. Resolutions of

reconstructed by SPASE, and

50 reconstructed by AMANDA (simulated p,He,O,and Fe nuclei all

included): (a) shower size resolution: The distribution of true total number of electrons is shown for events with

in the range 50–

55 m

and (b) muon energy resolution: the distribution of true total muon energy at the surface is given for a

50 in the range 0.9–1.1

photoelectron/OM.

572

J. Ahrens et al. / Astroparticle Physics 21 (2004) 565–581

SPASE track of an event to intersect a cylinder

of ice representing AMANDA’s geometrical

volume.

•

The shower core lies within the SPASE array

. The

shower core reconstruction and therefore the

entire event reconstruction is not reliable if

the core is located outside the array. The cut

removes about 10% of the data.

•

For small

showers, the track must pass clo-

ser to the center of AMANDA

. Angular resolu-

tion begins to suffer for small

when fewer

AMANDA modules are hit. However, tracks

which pass close to the center of AMANDA

can still be reconstructed well. Between

Þ¼

5 and 20 m

, the cut on track direction

is tightened linearly from 1.0 to 0.7 times the

geometrical size of AMANDA, in order to pre-

serve good angular resolution without losing

too many events.

•

The LDF fit slope is within a reasonable range

As discussed earlier, the reconstructed effective

propagation length

should resemble what

has been independently measured for antarctic

ice, but can take on a range of values and still

provide a robust

50. This slope is required

to be between zero and 100. This cut does not

have a large impact on the event statistics; it

merely removes unphysical outliers.

In 1998 SPASE recorded 28.9 million showers.

AMANDA’s ontime during that year was 70% of

SPASE’s. Out of the coincidentally recorded

events 16% were pointing at AMANDA and pas-

sed the

cut. 70,000 of those events

were succesfully reconstructed, and 5655 events

survive the additional quality cuts to the final

analysis level. From the Monte Carlo sample, 5515

events survive to this level.

6. Measuring cosmic ray energy and composition

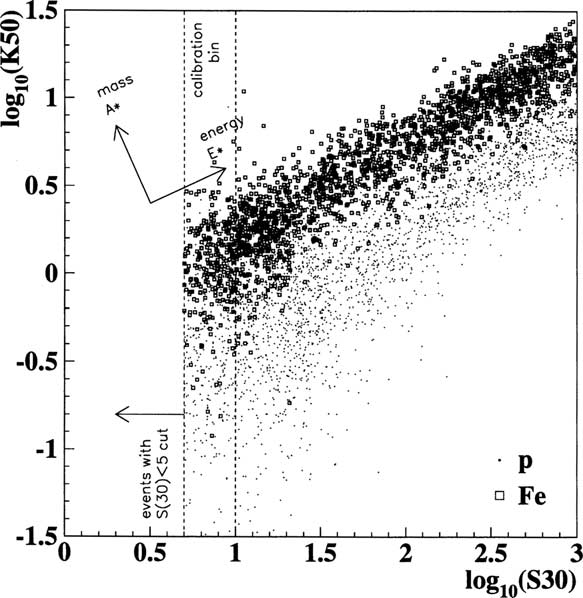
When the two observables

50 and

are

plotted against each other, as in Fig. 6, showers of

different primary energy and primary mass can be

separated in the two-dimensional parameter space.

The higher the primary energy of the event, the

more electrons in SPASE and the more muons in

AMANDA. But for a

given

primary energy, iron-

induced showers are more muon-rich than proton-

induced showers and

50 is enhanced relative to

. This can be explained in a simplified way by

the superposition principle; a shower from a nu-

cleus of mass

can be approximated as

super-

imposed proton-like showers, each with 1

of the

total primary energy. The larger the

, the smaller

the energy fraction carried by each nucleon, and

the lower the energies of secondary pions, which

are more likely to decay into muons before inter-

acting. Thus, heavy primaries produce more muons

for the same primary energy than light primaries.

We can create a set of transformed axes, named

and

, also shown in Fig. 6. These axes are

rotated from

50 and

(30) by an angle (deter-

mined by simulations) of 24

. Every event can now

be identified with coordinates in

space,

and these coordinates are used as energy and mass

estimators for that event.

Two more steps are necessary to get to a

determination of

itself. First, the absolute

scale of

50 (the more vulnerable of the two ob-

servables to systematic uncertainties) must be cal-

ibrated. This is done by calibrating the mass

Fig. 6.

vs. JFC50 for simulated proton and iron events.

The ‘‘calibration bin’’ of

between 5 and 10 m

, as well as

the directions of the

and

axes are indicated on the plot.

J. Ahrens et al. / Astroparticle Physics 21 (2004) 565–581

573

composition at low energies where direct mea-

surements are available. Second, the data and

Monte Carlo simulations are then compared along

the

and

axes to get the best fit mass com-

position in a series of energy bins.

The analysis presented here uses a 2-component

Monte Carlo model (proton and iron primaries).

The data are expected to lie somewhere in be-

tween, and the mean log mass

from a mix-

ture of protons and iron is used to characterize the

mass composition. A 4-component model (p, He,

O, and Fe) was also explored, and is used here as a

consistency check.

6.1. Calibrating with direct measurements at low

energy

To measure the absolute scale of

50 from

simulations alone suffers systematic uncertainties

from a variety of sources, for instance, the absolute

number of muons predicted by the hadronic inter-

action model or the muon propagation simulation.

These uncertainties affect the absolute calibration

of the

50 parameter, but not the shape or prop-

erties of its distribution. Cosmic ray composition is

known at low energies from direct measurements

up to several hundred TeV; if we calibrate the

measurement at low energies to agree with the

known composition, we can then investigate whe-

ther the composition

changes

as energy increases.

The technique is calibrated at low energies using

events with

Þ¼

5–10 m

, the vertical ‘‘slice’’

shown in Fig. 6, which corresponds to 200–350

TeV protons and about twice this energy for iron.

Monte Carlo events, which are generated over a

wide energy range using the same spectral index

for each component, are weighted by a relative

proportion which represents a mixed composition,

. This mean log mass at low energy can be

taken from direct measurements such as JACEE

[21] and RUNJOB [22]. Figure 19 of Ref. [22]

shows

of 2.1

0.2 measured by JACEE be-

tween 10

and 10

GeV and

i¼

measured by RUNJOB. We have taken a calibra-

tion value

i¼

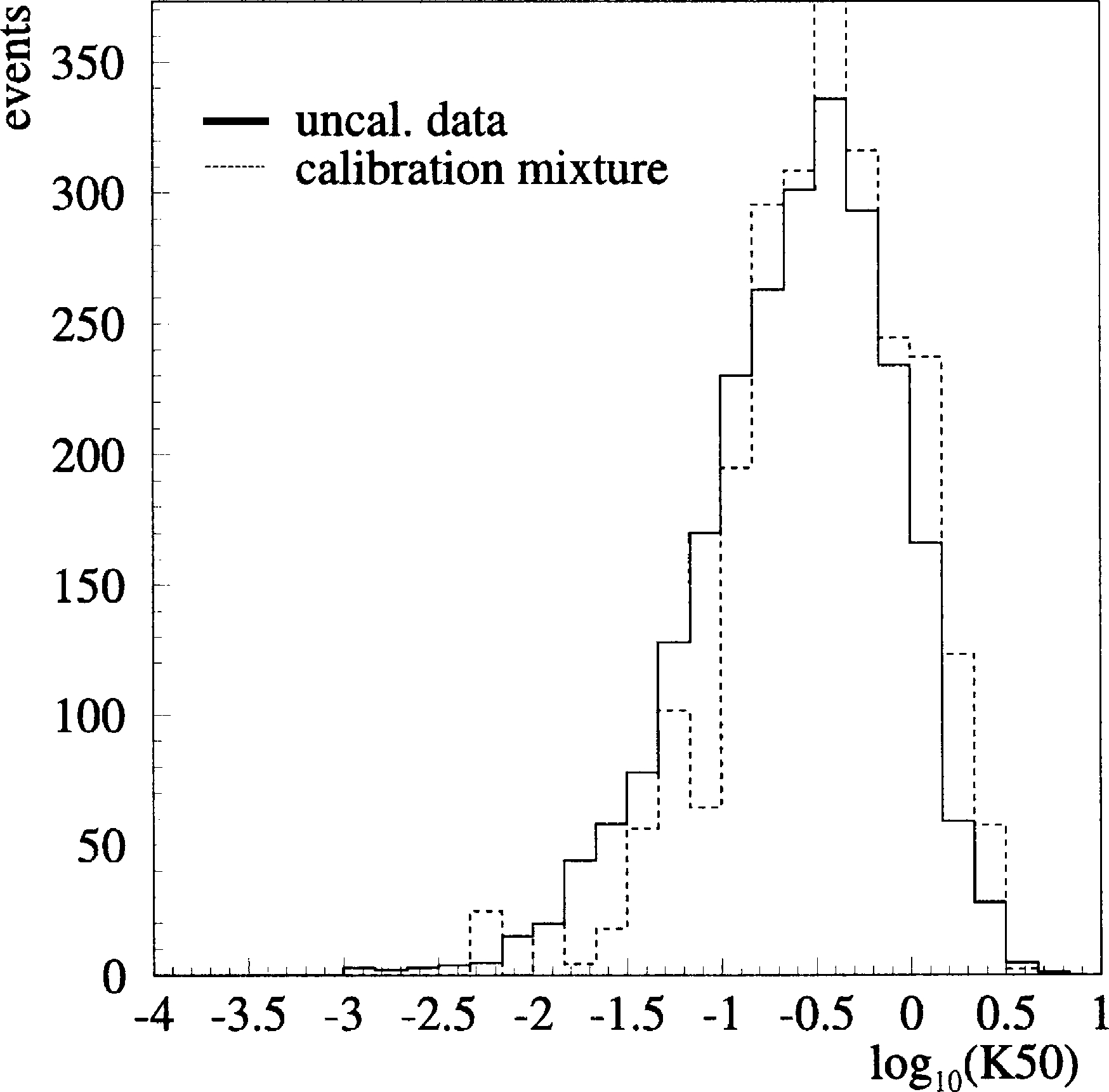
The distributions of log

for data and the

calibration mixture of simulated proton and iron

within this slice, shown in Fig. 7, agree well in

shape, but not in mean. Hypothesizing that data

and Monte Carlo differ by a constant offset

log

, we can find the value of

which makes

the two histograms agree best using a Kolmogo-

rov–Smirnov test. This renormalization factor is

applied to the log

of the data for the

remainder of this paper. For the baseline model,

is found to be 0.14. Alternative values of

were

also analyzed in order to investigate systematic

errors; these will be discussed later.

Fig. 8 shows both calibrated and uncalibrated

data in the

parameter space, together

with the simulated proton and iron events. Un-

calibrated, the data appear unphysically light

given our knowledge of mass composition at low

energies. Calibrated, the data reveal the trend in

mass composition. The seven slanted straight lines

drawn represent the constant energies of log

(

prim

GeV

Þ¼

6, 5.8, 6.0, 6.2, 6.4, 6.6, and 6.8.

They form six

bins

of constant energy. A formal

procedure for measuring energy and mass is de-

scribed below.

6.2. Energy resolution

The

axis is roughly linear in the log of

the true primary energy. Using simulations, we

Fig. 7. The distribution of log

(

50) for uncalibrated data and

the calibration mixture.

574

J. Ahrens et al. / Astroparticle Physics 21 (2004) 565–581

compare this energy estimator with the true pri-

mary energy log

(

prim

). The relationship is com-

position-independent, and can be fit by

log

prim

GeV

Þ¼

The resolution of this line fit is given in Table 1

for five different energy ranges with equal mixtures

of proton- and iron-induced showers:

12 in

log

prim

at energies near 100 TeV, and

improving 0.057 at the highest simulated energies

of 30 PeV. The combined detector’s response is

linear up to about 10 PeV. Fig. 9 shows the energy

resolution of proton- and iron-induced air showers

in the energy range from 1 to 10 PeV. The average

energy resolution is

07 in log

(

prim

6.3. Mass resolution

Just as

can be used to estimate primary en-

ergy,

can be used to estimate primary mass for

each shower. In particular, to measure cosmic ray

composition from the data, we compare the

distributions of the data and the Monte Carlo. The

proton and iron Monte Carlo events can be mixed

with an iron fraction

to reproduce a given

. The mixture which best describes the data is

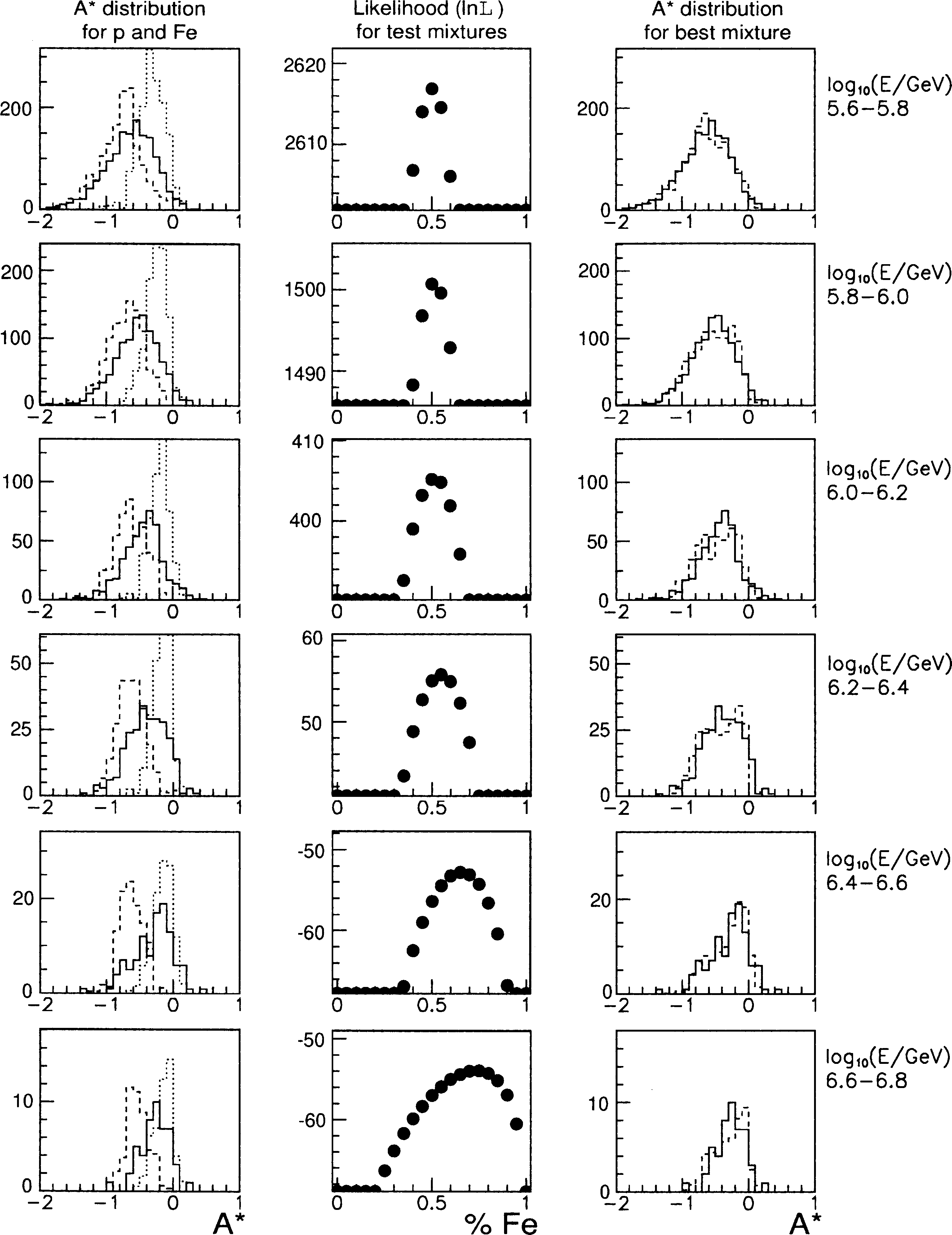
found by scanning through hypothesis mixtures,

such as those shown in Fig. 10. The likelihood

of each hypothesis

is the product over histo-

gram bins of the Poisson probability of observing

the number of data events given the number of

simulated events in that bin. The most likely

found at the peak of the resulting likelihood curve,

where

Þ¼

max

. The error on the measure-

ment can be derived from the width of the likeli-

hood curve; if

is Gaussian in

, then 1

is the

value of

at which [23]

Fig. 8. Uncalibrated and calibrated data, in the

parameter space, compared to simulated proton and iron

events. Constant-energy contours are also shown.

Table 1

Energy resolution of an equal mixture of p- and Fe-induced

showers as a function of energy based on full detector simula-

tion of both detectors

log

GeV

log

reco

true

5.0–5.5 0.010 0.119

5.5–6.0

)

0.041 0.113

6.0–6.5

)

0.035 0.072

6.5–7.0

)

0.014 0.059

7.0–7.5

)

0.026 0.057

Fig. 9. Distributions of the differences between reconstructed

and true energy of an equal mixture of p- and Fe-showers for

the energy range from 1 to 10 PeV. The width of the distribu-

tion measures the energy resolution. The results are based on

full shower and detector Monte Carlo simulations.

J. Ahrens et al. / Astroparticle Physics 21 (2004) 565–581

575

Þ¼

max

exp

max

The simulated histograms are normalized to the

data, so the test compares the histogram shapes.

The Kolmogorov–Smirnov test was also applied to

the histograms as a cross-check, with duplicate

results. The procedure was repeated for each of the

six energy bins; the results for all six bins are

shown in Fig. 11.

6.4. Systematic uncertainties

We are faced with a choice of different shower

generation, muon propagation, and detector

models, each with a different absolute normaliza-

tion. However, calibrating data to Monte Carlo in

a low-energy calibration bin is a technique adapt-

able to any model. By treating each model as an

independent test of normalization and composi-

tion, we can gauge the stability of this technique

under changing models, and estimate the system-

atic error on the final measurement. In addition

to a baseline model, several alternatives can serve

to test the robustness of the analysis to a variation

of parameters. The six models used here are

•

Baseline

. MOCCA/QGSJET, muon propagator

PROPMU, 17-layer ice, 2-component (p and

Fe) composition.

•

Bulk

. Same as baseline, but with uniform ice.

Here we use a simplified ice model which con-

tains no vertical structure.

•

Four component

. p, He, O and Fe nuclei, split

into light and heavy groups with equal weight

within each group.

•

SIBYLL

. The SIBYLL-17 code [24] is used for

the interaction model instead of QGSJET.

•

Amplitude gate

. Here, an incorrect amplitude

readout was used in simulating AMANDA

electronics, resulting in a loss of photon count-

ing accuracy. Using this model tests the sensitiv-

ity of the Monte Carlo to a perturbation in the

electronic response.

•

MMC

. The muon propagator PROPMU has

been replaced with the propagator MMC[25].

For each model, a calibration constant

was

computed, and an independent analysis performed

in the same fashion as described above. The same

experimental data were compared to each model in

the variable

, and the mean log mass and error

bars for the model were computed from the like-

lihood curve. The numerical results from the six

models are summarized in Table 2. While there are

Fig. 10. Sample composition mixtures of p- and Fe-induced showers (dashed), and how they can be compared to data (solid). The

double peak structure in the some mixtures illustrates the separation potential between p and Fe.

576

J. Ahrens et al. / Astroparticle Physics 21 (2004) 565–581

systematic shifts in the

absolute

between

different models, all of the composition measure-

ments follow a similar

trend

An additional source of systematic error is

uncertainty in the direct measurement at low

energy, against which the

50 parameter is

Fig. 11. For the six constant-energy bins: (left) distributions of

for pure protons (dashed), pure iron (dotted) and calibrated data

(solid); (middle) ln

as a function of iron percentage and (right) distributions of

for best mixture of protons and iron (dashed) and

calibrated data (solid). Monte Carlo distributions are normalized to data.

J. Ahrens et al. / Astroparticle Physics 21 (2004) 565–581

577

calibrated and the factor

computed. To study

this, a variety of different values of

from 0.04 to

0.18 (corresponding to direct measurement

values between 1.8 and 2.2) were tested. The re-

sults are included in the summary, as a distinct

source of error.

7. Results and discussion

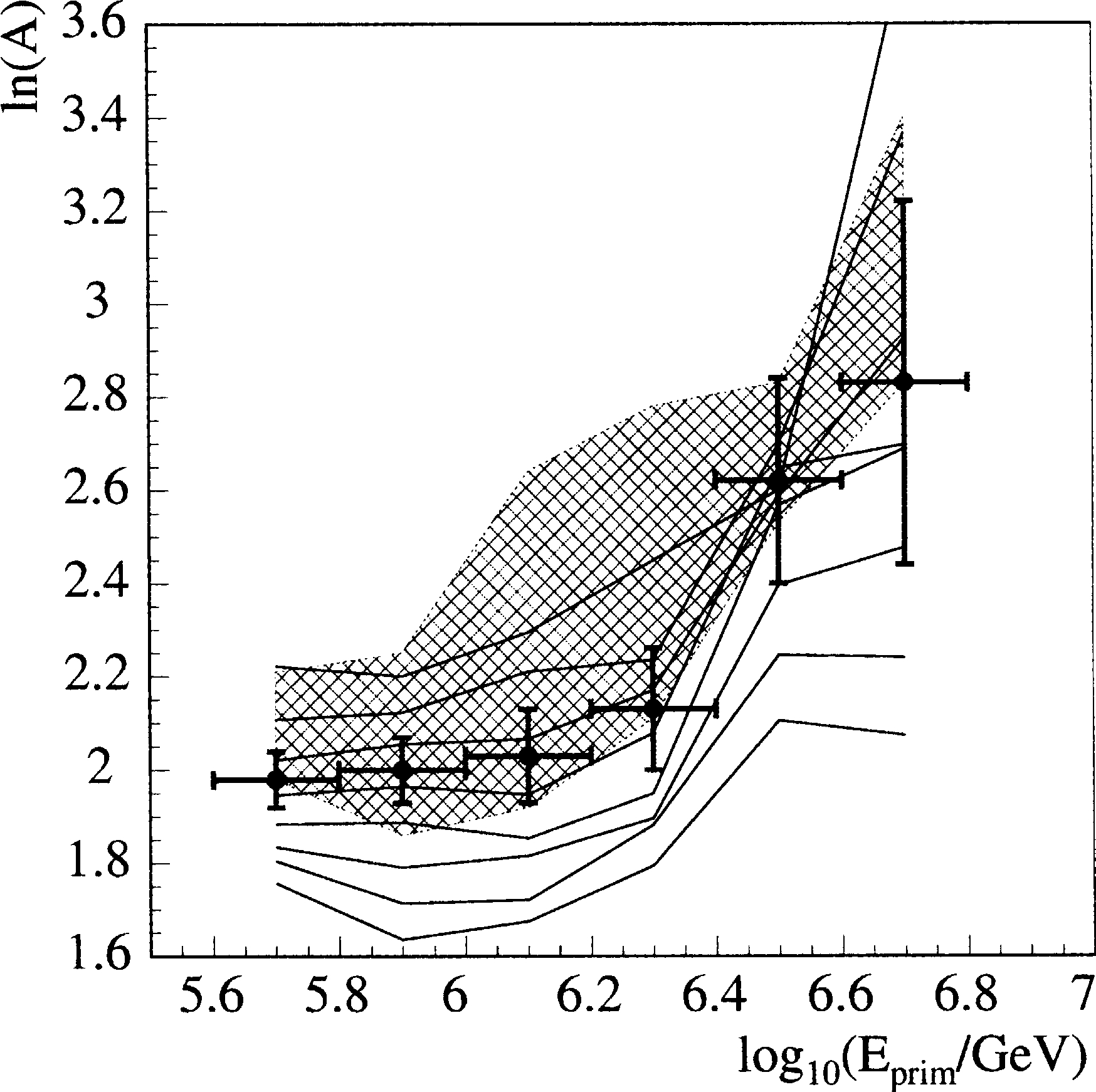
Fig. 12 shows the mean log mass as a function

of the primary energy. Data points indicate the

results from the baseline model, normalized to

i¼

0 in the normalization bin, with one

standard deviation statistical error bars computed

from the likelihood curve. The shaded band indi-

cates the range of results obtained using different

simulations, an estimate of the systematic error

from models. Note that these error bars are highly

asymmetric and the baseline model gives values

close to the lower limit. The additional lines indi-

cate results using different initial calibration mix-

tures, corresponding to

values from 0.04 to 0.18,

with the baseline simulation, an estimate of the

systematic error from our incomplete knowledge

at low energies.

The data show a mass composition consis-

tent with flat between 500 TeV and 1.2 PeV,

after which it starts to become heavier.

in-

creases by 0.9 between 1.2 and 6 PeV. The statis-

tical and systematic errors in the last bins are

too large to allow a good determination of

growth of

. The data are not consistent,

however, with mass becoming lighter through the

knee.

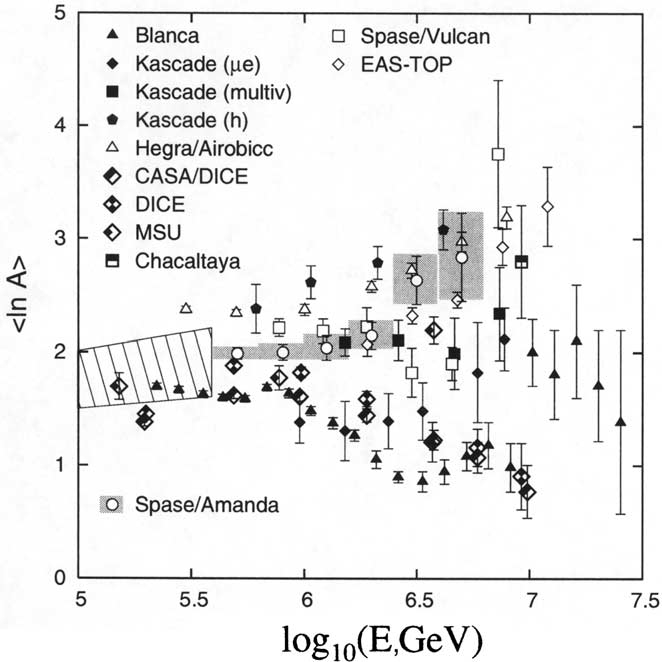
Fig. 13 compares our results with other pub-

lished values obtained with Cherenkov telescopes,

scintillators, and a variety of coincidence experi-

ments. Our results are consistent with most of the

other results that measure cosmic ray composition

becoming heavier with energy. These include the

air shower experiments KASCADE, MSU and

Chacaltaya, the Cherenkov light experiment HE-

GRA/AIROBICC, and the air-shower––deep

Table 2

Summary of composition results from different simulation models

Model Baseline Bulk 4 Comp. SIBYLL Ampl. gate MMC

0.14 0.06 0.10 0.01 0.14 0.16

log

(

/GeV)

Þh

5.6–5.8 1.98

0.06 (0.13) 2.09 1.86 2.08 1.99 2.21

5.8–6.0 2.00

0.07 (0.14) 2.05 1.91 1.86 2.00 2.15

6.0–6.2 2.03

0.10 (0.21) 2.22 2.42 1.92 2.03 2.36

6.2–6.4 2.13

0.13 (0.26) 2.11 2.61 2.13 2.15 2.24

6.4–6.6 2.62

0.22 (0.45) 2.53 2.61 * 2.56 2.67

6.6–6.8 2.83

0.39 (0.78) 2.87 3.40 * 2.83 3.2

The asterisk indicates omission due to lack of simulated statistics.

Fig. 12. Change of the mass composition relative to the base-

line model as a function of the energy. Error bars represent

statistical 1

errors. Shaded region indicates systematic errors

around these center values, defined as the envelope of maximum

deviation in

when using the six perturbations of the

baseline simulation. Additional lines show results using alter-

native values of

with the baseline model.

578

J. Ahrens et al. / Astroparticle Physics 21 (2004) 565–581

underground muon telescope EAS-TOP/MACRO.

SPASE/AMANDA result is in conflict only with

the results of BLANCA and DICE (both Cher-

enkov telescopes) which show the mass becoming

lighter in this energy region.

Although each experiment alone has small sta-

tistical error bars (as can be seen in Fig. 13), sys-

tematic errors are often significant and not

displayed in the figure. One can see that many

results do not overlap with each other at low

energies where there is overlap with direct experi-

ments, suggesting differences in systematic errors

between experiments and making them difficult to

compare. Systematic errors are a challenge that all

experiments have in common, which in many cases

dominate the conclusion.

SPASE/AMANDA data indicate an increase of

the mass in the energy range from 1 to 6 PeV and

improve the current knowledge of the mass com-

position in the region of the knee. This result is

significant because the technique and its sources of

systematic error are unique. First, the muon sur-

face energy threshold for detection at depth is

about 300 GeV due to the 1500 to 2000 m of solid

ice overburden above the detector. This is high

enough for sensitivity to the muons created in the

first interactions, yet low enough to overlap with

direct measurements for mass composition cali-

bration. Second, the entire high-energy muon

bundle is measured over a large volume, and the

light output from all muons is sampled over a

track length of 500 m and laterally out to 150 m.

For a PeV iron primary, AMANDA collects a

hundred to several thousand photons over a large

volume, allowing a measurement of the total muon

bundle energy loss. As a result the combined

detectors achieve a mass-independent relative en-

ergy resolution of 0.07 in log

(

prim

/GeV). This

analysis is also not sensitive to details of the

implementation of the photon propagation, be-

cause

50 measures the light intensity at a con-

stant distance from the muon track. The primary

interaction model and the muon propagator are

probed only for the difference between proton- and

iron-induced showers and their energies. Thus, the

method of probing the relative change of muonic

(hadronic) energy to electromagnetic energy in the

air shower is robust and model independent. The

Fig. 13. SPASE/AMANDA composition results compared to other experiments, taken or adapted from [5,10,26–30]. Limits from

direct measurements at low energy are shown as lines.

J. Ahrens et al. / Astroparticle Physics 21 (2004) 565–581

579

location of the SPASE site at high altitude is

advantageous for the electron component, because

the shower maximum is closer to the detector and

fluctuations are not as strong as they are at sea

level.

However, there is room for improvement. Re-

cent data taken with the larger AMANDA-II

array will substantially increase the data statistics.

The rate of coincident events between SPASE-2

and AMANDA-II is increased by a factor of 2–3.

IceCube [31], the next generation neutrino tele-

scope currently in preparation will include a sur-

face array of one square kilometer in size

(

m sr). Simulations indicate that both the size

and technology will be adequate to measure the

mass composition up to 10

eV, well beyond any

current result.

Acknowledgements

This research was supported by the following

agencies: National Science Foundation: Office of

Polar Programs, National Science Foundation-

Physics Division, University of Wisconsin Alumni

Research Foundation, Department of Energy, and

National Energy Research Scientific Computing

Center (supported by the Office of Energy Re-

search of the Department of Energy), UC-Irvine

AENEAS Supercomputer Facility, USA; Swedish

Research Council, Swedish Polar Research Secre-

tariat, and Knut and Alice Wallenberg Founda-

tion, Sweden; German Ministry for Education and

Research, Deutsche Forschungsgemein-schaft

(DFG), Germany; Fund for Scientific Research

(FNRS-FWO), Flanders Institute to encourage

scientific and technological research in industry

(IWT), and Belgian Federal Office for Scientific,

Technical and Cultural affairs (OSTC), Belgium;

Particle Physics and Astronomy Research Council,

UK; D.F.C. acknowledges the support of the NSF

CAREER program.

References

[1] J.E. Dickinson et al., Nucl. Instrum. Methods A 440 (2000)

95.

[2] J. Ahrens et al., AMANDA Collaboration, Phys. Rev. D

66 (2002) 012005.

[3] K. Greisen, Progr. Cosm. Ray Phys. 3 (1956) 1.

[4] A. Walker et al., Nucl. Instrum Methods A 301 (1991)

574.

[5] J. Hinton, Ph.D. dissertation, University of Leeds,

1998.

[6] J. Ahrens et al., (AMANDA Collaboration), Muon track

reconstruction and data selection techniques in AMAN-

DA, Nucl. Instrum. Methods A 524 (2004) 169.

[7] M. Aglietta et al., EAS-TOP and MACRO Collaborations,

Phys. Lett. B 337 (1994) 376.

[8] G. Navarra et al., EAS-TOP and LVD Collaborations,

Nucl. Phys. B. Proc. Suppl. 70 (1999) 512.

[9] M. Aglietta et al., EAS-TOP and LVD Collaborations,

Astropart. Phys. 9 (1998) 185.

[10] M. Aglietta et al., Astropart. Phys. 20 (2004) 641.

[11] T. Gaisser, Cosmic Rays and Particle Physics, Cambridge

University Press, 1990.

[12] R.M. Barnett et al., Particle Data Group, Phys. Rev. D 54

(1996) 1.

[13] K. Woschnagg et al., (The AMANDA Collaboration), in:

Proceedings of the of the 26th ICRC, Salt Lake City 2,

1999, p. 200.

[14] K. Woschnagg, private communication.

[15] Y.D. He, P.B. Price, J. Geophys. Res. 103 (1998)

17041.

[16] P. Askebjer et al., Appl. Opt. 36 (1997) 4168.

[17] J. Ahrens et al., (AMANDA and SPASE Collaborations),

Calibration and survey of AMANDA with the

SPASE detectors, Nucl. Instrum. Methods A 522 (2004)

347.

[18] A.M. Hillas, in: Proceedings of the 24th International

Cosmic Ray Conference, Rome, vol. 1, 1995, p. 270.

[19] N.N. Kalmykov, S.S. Ostapchenko, Phys. At. Nucl. 56 (3)

(1993) 346;

N.N. Kalmykov, S.S. Ostapchenko, A.I. Pavlov, Nucl.

Phys. B (Proc. Suppl.) 52B (1997) 17.

[20] P. Lipari, T. Stanev, Phys. Rev. D 44 (1991) 3543.

[21] K. Asakimori (The JACEE Collaboration), in: Pro-

ceedings of the 23rd ICRC (Calgary), vol. 2, 1993, p. 21,

25.

[22] A.V. Apanasenko et al., Astropart. Phys. 16 (2001)

13.

[23] P.R. Bevington, D.K. Robinson, Data Reduction and

Error Analysis for the Physical Sciences, McGraw-Hill,

New York, 1969.

[24] R.S. Fletcher, T.K. Gaisser, P. Lipari, T. Stanev, Phys.

Rev. D 50 (1994) 5710;

J. Engel, T.K. Gaisser, P. Lipari, T. Stanev, Phys. Rev. D

46 (1992) 5013.

[25] W. Rhode, D. Chirkin, in: Proc. of the 27th ICRC

(Hamburg), 2001, p. HE220.

[26] A. Castellina, Nucl. Phys. Proc. Suppl. 97 (2001) 35.

[27] F. Arqueros et al., A&A 359 (2000) 682.

[28] S.P. Swordy et al., Astropart. Phys. 18 (2002) 129–150,

astro-ph/0202159.

580

J. Ahrens et al. / Astroparticle Physics 21 (2004) 565–581

[29] K.-H. Kampert, Invited paper at Vulcano Workshop 2002,

astro-ph/0212348.

[30] A. Haungs, H. Rebel, M. Roth, Rept. Prog. Phys. 66

(2003) 1145.

[31] J. Ahrens et al., The IceCube Proposal to NSF (2000);

J. Ahrens et al., PDD: IceCube Conceptual Design

Document (2001). Available from <http://ice-

cube.wisc.edu>.

J. Ahrens et al. / Astroparticle Physics 21 (2004) 565–581

581