PII: S0927-6505(99)00092-4

Astroparticle Physics 13 2000 1–20

www.elsevier.nl

locate

astropart

The AMANDA neutrino telescope: principle of operation and

first results

E. Andres

, P. Askebjer

, S.W. Barwick

)

, R. Bay

, L. Bergstrom

, A. Biron

J. Booth

, A. Bouchta

, S. Carius

, M. Carlson

, D. Cowen

, E. Dalberg

T. DeYoung

, P. Ekstrom

, B. Erlandson

, A. Goobar

, L. Gray

, A. Hallgren

F. Halzen

, R. Hardtke

, S. Hart

,Y.He

, H. Heukenkamp

, G. Hill

P.O. Hulth

, S. Hundertmark

, J. Jacobsen

, A. Jones

, V. Kandhadai

, A. Karle

B. Koci

, P. Lindahl

, I. Liubarsky

, M. Leuthold

, D.M. Lowder

P. Marciniewski

, T. Mikolajski

, T. Miller

, P. Miocinovic

, P. Mock

R. Morse

, P. Niessen

, C. Perez de los Heros

, R. Porrata

, D. Potter

P.B. Price

, G. Przybylski

, A. Richards

, S. Richter

, P. Romenesko

H. Rubinstein

, E. Schneider

, T. Schmidt

, R. Schwarz

, M. Solarz

G.M. Spiczak

, C. Spiering

, O. Streicher

, Q Sun

, L. Thollander

T. Thon

, S. Tilav

, C. Walck

, C. Wiebusch

, R. Wischnewski

K. Woschnagg

, G. Yodh

Bartol Research Institute, Uni

ersity of Delaware, Newark, DE, USA

DESYZeuthen, Zeuthen, Germany

Kalmar Uni

ersity, Sweden

Stockholm Uni

ersity, Stockholm, Sweden

Uni

ersity of California Berkeley, Berkeley, CA, USA

Uni

ersity of California Ir

ine, Ir

ine, CA, USA

Uni

ersity of Pennsyl

ania, Philadelphia, PA, USA

Uni

ersity of Wisconsin, Madison, WI, USA

Lawrence Berkeley Laboratory, Berkeley, CA, USA

South Pole Station, Antarctica

Uni

ersity of Uppsala, Uppsala, Sweden

Received 25 May 1999; accepted 21 June 1999

Abstract

AMANDA is a highenergy neutrino telescope presently under construction at the geographical South Pole. In the

. .

Antarctic summer 1995

96, an array of 80 optical modules OMs arranged on 4 strings AMANDAB4 was deployed at

)

Corresponding author.

Email address:

sbarwick@uci.edu S.W. Barwick .

09276505

$ see front matter

PII: S0927 6505 99 000924

()

E. Andres et al.

Astroparticle Physics 13 2000 1–20

depths between 1.5 and 2 km. In this paper we describe the design and performance of the AMANDAB4 prototype, based

on data collected between February and November 1996. Monte Carlo simulations of the detector response to downgoing

atmospheric muon tracks show that the global behavior of the detector is understood. We describe the data analysis method

and present first results on atmospheric muon reconstruction and separation of neutrino candidates. The AMANDA array

was upgraded with 216 OMs on 6 new strings in 1996

97 AMANDAB10 , and 122 additional OMs on 3 strings in

1997

98.

1. Introduction

Techniques are being developed by several groups

to use high energy neutrinos as a probe for the

highest energy phenomena observed in the Universe.

Neutrinos yield information complementary to that

obtained from observations of high energy photons

and charged particles since they interact only weakly

and can reach the observer unobscured by intervent

ing matter and undeflected by magnetic fields.

The primary mission of large neutrino telescopes

is to probe the Universe in a new observational

window and to search for the sources of the highest

energy phenomena. Presently suggested candidates

for these sources are, for instance, Active Galactic

. .

Nuclei AGN and Gamma Ray Bursts GRB . A

neutrino signal from a certain object would consti

tute the clearest signature of the hadronic nature of

that cosmic accelerator 1 . Apart from that, neutrino

telescopes search for neutrinos produced in annihila

tions of Weakly Interacting Massive Particles

WIMPs which may have accumulated in the center

of the Earth or in the Sun. WIMPS might contribute

to the cold dark matter content of the Universe, their

detection being of extreme importance for cosmol

ogy 2,3 . Neutrino telescopes can be also used to

monitor the Galaxy for supernova explosions 4 and

to search for exotic particles like magnetic monopoles

5,6 . In coincidence with surface air shower arrays,

deep neutrino detectors can be used to study the

chemical composition of charged cosmic rays. Fi

nally, environmental investigations – oceanology or

limnology in water, glaciology in ice – have proved

to be exciting applications of these devices 7,9 .

Planned highenergy neutrino telescopes differ in

many aspects from existing underground neutrino

detectors. Their architecture is optimized to achieve

a large detection area rather than a low energy

threshold. They are deployed in transparent ‘‘open’’

media like water in oceans or lakes, or deep polar

ice. This brings additional inherent technological

challenges compared with the assembly of a detector

in an accelerator tunnel or underground cavities.

Neutrinos are inferred from the arrival times of

Cherenkov light emitted by charged secondaries pro

duced in neutrino interactions. The light is mapped

by photomultiplier tubes PMTs spanning a coarse

threedimensional grid.

The traditional approach to muon neutrino detec

tion is the observation of upward moving muons

produced in charged current interactions in the rock,

water or ice below the detector. The Earth is used as

a filter with respect to atmospheric muons. Still,

suppression of downwardgoing muons is of top

importance, since their flux exceeds that of upward

going muons from atmospheric neutrinos by several

orders of magnitude.

An array of PMTs can also be used to reconstruct

the energy and location of isolated cascades due to

neutrino interactions. Burstlike events, like the onset

of a supernova, might be detected by measuring the

increased count rates of all individual PMTs.

Technologies for under

water

telescopes have been

pioneered by the since decommissioned DUMAND

project near Hawaii 11,12 and by the Baikal collab

oration 7,10 . In contrast to these approaches, the

AMANDA detector 15 used deep polar ice as target

and radiator. Two projects in the Mediterranean,

wx wx

NESTOR 13 and ANTARES 14 , have joined the

worldwide effort towards largescale underwater

telescopes. BAIKAL and AMANDA are presently

taking data with first stage detectors.

The present paper describes results obtained with

the first four out of the current thirteen strings of

the AMANDA detector. The paper is organized as

follows: In Section 2 we give a general overview of

()

E. Andres et al.

Astroparticle Physics 13 2000 1–20

the AMANDA concept. Section 3 summarizes the

results obtained with a shallow survey detector called

AMANDAA. Section 4 describes the design of the

first four strings of the deeper array AMANDAB4.

Calibration of time response and of geometry are

explained in Section 5. In Section 6 we describe the

simulation and reconstruction methods with respect

to atmospheric muons and compare experimental

data to Monte Carlo calculations. Section 7 demon

strates the performance of AMANDAB4 operated in

coincidence with SPASE, a surface air shower array.

In Section 8, the angular spectrum of atmospheric

muons is derived and transformed into a dependence

of the vertical intensity on depth. Section 9 describes

the separation of first upward going muon candi

dates. Finally, a summary of the status of AMANDA

and results is presented in Section 10.

2. The AMANDA concept

AMANDA Antarctic Muon And Neutrino Detec

tor Array uses the natural Antarctic ice as both

target and Cherenkov medium. The detector consists

of strings of optical modules OMs frozen in the 3

km thick ice sheet at the South Pole. An OM consists

of a photomultiplier in a glass vessel. The strings are

deployed into holes drilled with pressurized hot wa

ter. The water column in the hole then refreezes

within 35–40 hours, fixing the string in its final

position. In our basic design, each OM has its own

cable supplying the high voltage HV as well as

transmitting the anode signal. The components under

the ice are kept as simple as possible, all the data

acquisition electronics being housed in a building at

the surface. The simplicity of the components under

ice and the nonhierarchical structure make the de

tector highly reliable.

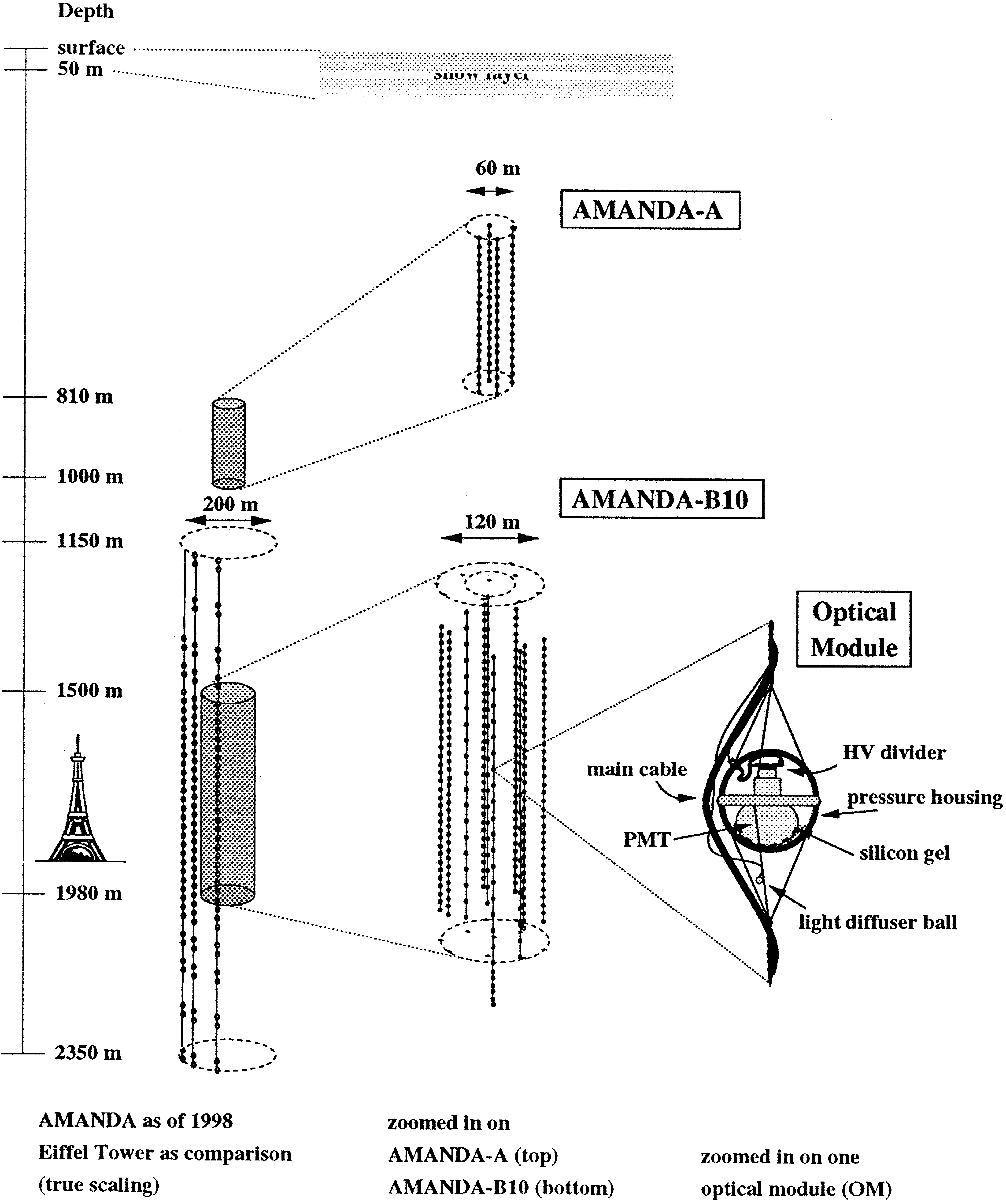
Fig. 1 shows the current configuration of the

AMANDA detector. The shallow array, AMANDA

A, was deployed at a depth of 800 to 1000 m in

1993

94 in an exploratory phase of the project.

Studies of the optical properties of the ice carried out

with AMANDAA showed that a high concentration

of residual air bubbles remaining at these depths

leads to strong scattering of light, making accurate

track reconstruction impossible 8 . Therefore, in the

polar season 1995

96 a deeper array consisting of

80 OMs arranged on four strings AMANDAB4

was deployed at depths ranging from 1545 to 1978

meters, where the concentration of bubbles was pre

dicted to be negligible according to extrapolation of

AMANDAA results. The detector was upgraded in

1996

97 with 216 additional OMs on 6 strings. This

detector of 4

6 strings was named AMANDAB10

and is sketched at the right side of Fig. 1.

AMANDAB10 was upgraded in the season 1997

by 3 strings instrumented between 1150 m and 2350

m which fulfill several tasks. Firstly, they explore

the very deep and very shallow ice with respect to a

future cube kilometer array. Secondly, they form one

corner of AMANDAII which is the next stage of

AMANDA with altogether about 700 OMs. Thirdly,

they have been used to test data transmission via

optical fibers.

There are several advantages that make the South

Pole a unique site for a neutrino telescope:

The geographic location is unique: A detector

located at the South Pole observes the northern

hemisphere, and complements any other of the

planned or existing detectors.

Ice is a sterile medium. The noise is given only

by the PMT dark noise and by

K decays in the

glass housings, which are 0.5–1.5 kHz for the

PMTs and spheres we used. Ocean and lake

experiments have to cope with 100 kHz noise

rates due to bioluminescence or K decays 25–

30 kHz if normalized to the photocathode area of

the 8 PMT used in AMANDA . This fact not

only facilitates counting rate experiments like the

search for low energy neutrinos from supernovae

or GRBs, but also leads to fewer accidental hits in

muon events – an essential advantage for trigger

formation and track reconstruction.

AMANDA can be operated in coincidence with

air shower arrays located at the surface. Apart

from complementing the information from the

surface arrays by measurements of muons pene

trating to AMANDA depths, the air shower infor

mation can be used to calibrate AMANDA.

The South Pole station has an excellent infrastruc

ture. Issues of vital importance to run big experi

()

E. Andres et al.

Astroparticle Physics 13 2000 1–20

Fig. 1. Scheme of the 1998 AMANDA installations. The left picture is drawn with true scaling. A zoomed view on AMANDAA top and

AMANDAB10 bottom is shown at the center. The right zoom depicts the optical module.

ments like transportation, power supply, satellite

communication and technical support are solved

and tested during many years of operation. Part of

an existing building can be used to house the

surface electronics.

The drilling and deployment procedures are tested

and well under control. AMANDA benefits from

the drilling expertise of the Polar Ice Coring

Office PICO . Currently about five days are

needed to drill a hole and to deploy a string with

PMTs to a depth of 2000 m. Future upgrades of

the drilling equipment are expected to result in a

further speedup.

The optical properties of the ice turned out to be

very different from what had been expected before

the AMANDAA phase. Whereas absorption is much

weaker than in oceans, scattering effects turned out

to be much stronger. Even at depths below 1400

meters, where residual bubbles have collapsed al

most completely into air hydrates, scattering is nearly

an order of magnitude stronger than in water see

below . Since scattering of light smears out the

arrival times of Cherenkov flashes, a main question

was whether under these conditions track reconstruc

tion was possible. As shown below, the answer is

yes.

()

E. Andres et al.

Astroparticle Physics 13 2000 1–20

3. AmandaA: a first survey

Preliminary explorations of the site and the drilling

technology were performed in the Antarctic Summer

1991

92 15 . During the 1993

94 campaign, four

strings each carrying 20 OMs ‘‘AMANDAA’’

were deployed between 800 and 1000 m depth. None

of the 73 OMs equipped with 8 EMI PMTs

surviving the refreezing process failed during the

following two years, giving a mean time between

failures MTBF

)

40 years for individual OMs in

AMANDAA. The OMs are connected to the surface

electronics by coaxial cables. Along with the coaxial

cables, optical fibers carry light from a Nd:YAG

laser at the surface to nylon light diffusers placed

about 30 cm below each PMT see Fig. 1 . Time

calibration is performed by sending nanosecond laser

pulses to individual diffusers and measuring the pho

ton arrival time distributions at the closest PMT.

From the distribution of the arrival times at

distant

PMTs, the optical properties of the medium were

derived 8,9 . The measured timing distributions in

dicated that photons do not propagate along straight

paths but are scattered and considerably delayed due

to residual bubbles in the ice. The distributions could

be fitted well with an analytic function describing

the threedimensional random walk scattering in

cluding absorption. These results showed that polar

ice at these depths has a very large absorption length,

exceeding 200 m at a wavelength of 410 nm. Scatter

ing is described by the effective scattering length

cos

, where

is the geometri

eff sc sc

cal scattering length and cos

the average cosine

of the scattering angle 8 .

increases with depth,

eff

from 40 cm at 830 m depth to 80 cm at 970 m. In

accordance with measurements at the Vostok Station

East Antarctica 16 and Byrd Station West

Antarctica these results suggested that at depths

greater than 1300–1400 m the phase transformation

from bubbles into airhydrate crystals would be com

plete and bubbles would disappear.

Although not suitable for track reconstruction,

AMANDAA can be used as a calorimeter for en

ergy measurements of neutrinoinduced cascadelike

events 18 . It is also used as a supernova monitor

17 . Events that simultaneously trigger AMANDAA

and the deeper AMANDAB have been used for

methodical studies like the investigation of the opti

cal properties of the ice or the assessment of events

with a lever arm of one kilometer.

4. Deployment and design of AMANDAB4

4.1. Drilling and deployment procedure

Drilling is performed by melting the ice with

pressurized water at 75

C. The drilling equipment

operates at a power of 1.9 MW and the typical drill

speed is about 1 cm

s. It takes about 3.5 days to

drill a 50–60 cm diameter hole to 2000 m depth.

In the season 1995

96, we drilled four holes, the

deepest of them reaching 2180 m. It took typically 8

hours to remove the drill and the water recycling

pump from the completed hole. The deployment of

one string with 20 OMs and several calibration

devices took about 18 hours with a limit of 35 hours

set by the refreezing of the water in the hole .

Several diagnostic devices allow monitoring of

the mechanical and thermal parameters during the

entire refreezing process and afterwards. It was

shown that the temperature increases with depth in

good agreement with the prediction of a standard

heat flow calculation for South Pole ice. At the

greatest depth, the temperature of the ice is

C, about 20

warmer than at the surface. Dur

ing the refreezing, the pressure reached a maximum

of 460 atm, more than twice the hydrostatic pressure

which is asymptotically established.

4.2. Detector design

The four strings of AMANDAB4 were deployed

at depths between 1545 and 1978 m. An OM con

sists of a 30 cm diameter glass sphere equipped with

Hamamatsu R59122 photomultiplier, a 14dy

node version of the standard 12dynode R5912 tube.

The PMTs are operated at a gain of 10

in order to

drive the pulses through 2 km of coaxial cable

without insitu amplification. The amplitude of a

onephotoelectron pulse is about 1 V. The coaxial

cable is also used for the HV supply, with the

advantage that only one cable and one electrical

penetrator into the sphere are required for each OM.

The measured noise rate of the AMANDAB4 PMTs

is typically 400 Hz threshold 0.4 photoelectrons .

()

E. Andres et al.

Astroparticle Physics 13 2000 1–20

Fig. 2. AMANDAB4: Top view, with distances between strings

given in meters, and side view showing optical modules and

calibration light sources. Upward looking PMTs are marked by

arrows.

The photocathode is in optical contact with the

glass sphere by the use of silicon gel. The transmis

sion of the glass of the pressure sphere is about 90%

in the spectral range between 400 and 600 nm; the

50% cutoff on the UV side is at about 365 nm. The

glass spheres are designed to withstand pressures of

about 660 atm.

Each string carries 20 OMs with a vertical spac

ing of 20 m. The fourth string carries six additional

OMs connected by a twisted pair cable. These six

OMs will not be used in the analyses presented in

this paper.

Fig. 2 shows a schematic view of AMANDAB4.

All PMTs look down with the exception of

1, 10

in strings 1 to 3 and

1, 2, 10, 19, 20 in string 4

with the numbers running from top to bottom of a

string . Strings 1–3 form a triangle with side lengths

77–67–61 m; string 4 is close to the center. The

OMs are arranged at depths 1545–1925 m string 1 ,

. .

1546–1926 m string 2 , 1598–1978 m string 3

and 1576–1956 m string 4 . The additional six OMs

equipped with twisted pair cables are at string 4

between 2009 and 2035 m. Seven of the 80 PMTs

which define AMANDAB4 were lost due to over

pressure and shearing forces to the electrical connec

tors during the refreezing period. These losses can be

reduced by computer controlled drilling avoiding

strong irregularities in the hole diameter, and by

improved connectors. Another 3 PMTs failed in the

course of the first 3 years of operation, giving a

MTBF of 73 years.

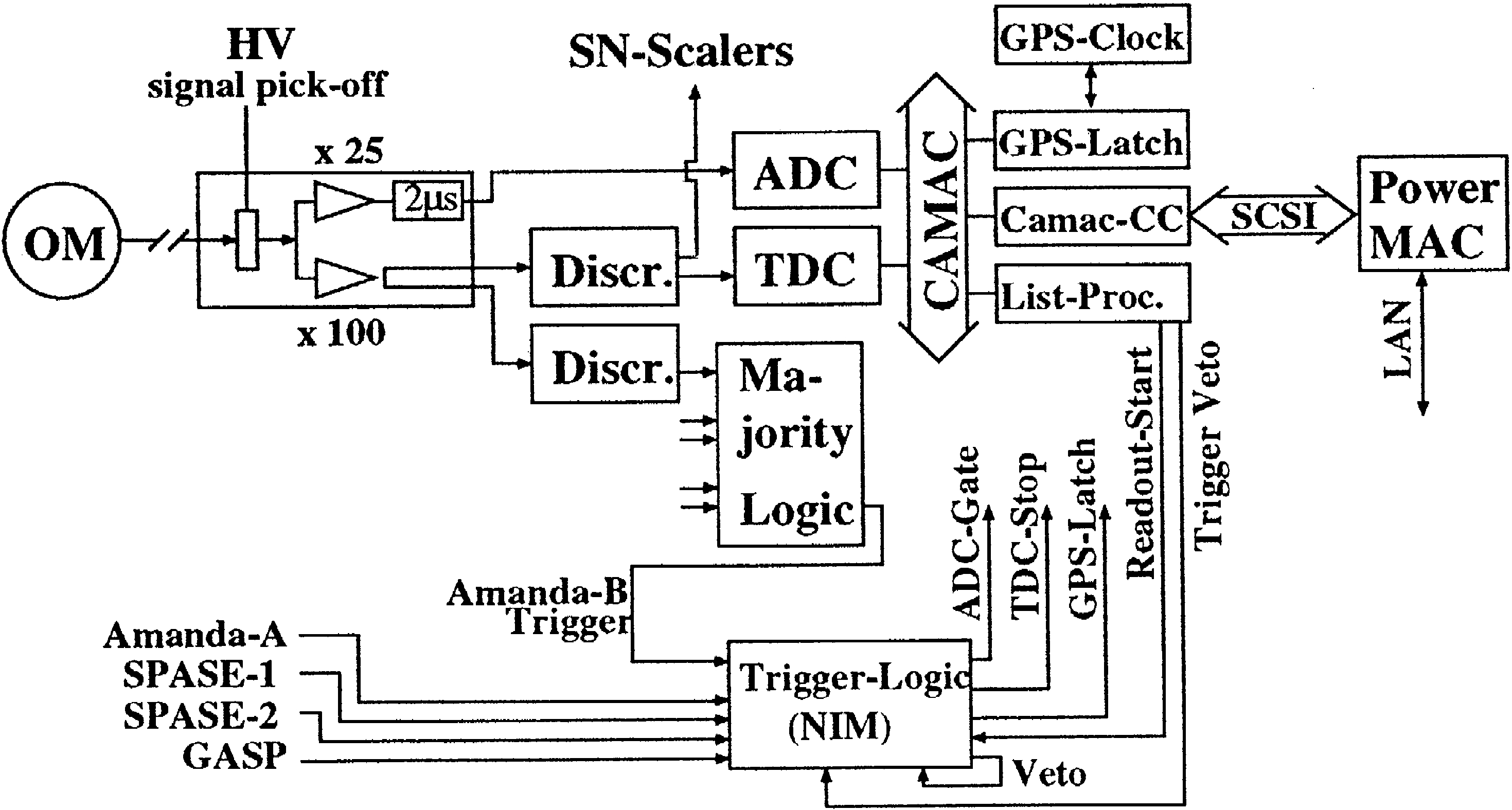
4.3. Electronics and DAQ

Each PMT can give a series of pulses which can

be resolved if separated from each other by more

than a few hundred nanoseconds. The data recorded

consist of the leading and trailing edges of the

pulses. The timeoverthreshold gives a measure of

the amplitude of individual pulses. Another measure

of the amplitude is obtained by a voltage sensitive

ADC which records the peak value out of the subse

quent hits of an event in a PMT. Actually, the

information consists of leading and trailing edges of

the last 8 resolved pulses, and of the largest ampli

tude of those of them which lie in a 4

sec window

centered at the array trigger time. Also recorded is

the GPS time at which the event occurred. A scheme

of the AMANDA electronics layout is shown in Fig.

The signal from each cable is fed to a module

consisting of a DC blocking highpass filter which

picks up the pulse, a fanout sending it to 2 ampli

fiers with 100

and 25

gain, and a 2

sec delay

for the lowgain signal.

The delayed signal is sent to a Phillips 7164 peak

sensing ADC. The other pulse is split and sent to

Fig. 3. DAQ system used for AMANDAB4 during 1996

()

E. Andres et al.

Astroparticle Physics 13 2000 1–20

LeCroy 4413 discriminators with thresholds set at

100 mV corresponding to about 0.3–0.4 photoelec

trons at the given high voltage. One of the resulting

ECL pulses is fed into a LeCroy 3377 TDC while

the other is sent to the majority trigger. The TDC

records the last 16 time edges occurring within a 32

sec time window.

The majority logic requests

8 hit PMTs within

a sliding window of 2

sec. The trigger produced by

this majority scheme is sent to the NIM trigger logic.

The latter accepts also triggers from AMANDAA or

the air shower experiments SPASE1, SPASE2 and

GASP. Thus AMANDA also records data when

these detectors trigger even if a proper AMANDA

trigger is not fulfilled. The total trigger rate during

1996 was about 26 Hz on average. The coincidences

from the other detectors contributed about 8 Hz to

the total rate.

The differences in cable length are not compen

sated before triggering. Therefore the true trigger

window would be about 300 nsec for a vertically

upgoing relativistic particle and

sec for a

downgoing one. As a result downgoing particles are

suppressed compared to upgoing.

Upon triggering, an ADC gate of 4

sec width is

formed, a stop signal is sent to the TDCs and a

readout signal is sent to a Hytec LP1341 list proces

sor. Then a veto lasting several microseconds in

hibits further trigger signals.

A separate system ‘‘SN scalers’’ in Fig. 3 moni

tors the counting rates of individual PMTs and

searches for rate excesses lasting several seconds.

Such an increase would be expected for multiple

lowenergy neutrino interactions close to each PMT

due to a supernova burst 4,17 .

The AMANDAB4 DAQ was running on a Mac

Intosh Power PC communicating through a SCSI bus

with the CAMAC crate controller. From the distribu

tion of the time differences between subsequent

events, the dead time of the DAQ is estimated to be

about 12%. The MacIntosh has been replaced by a

PentiumII PC running under LINUX in 1998, and

part of the CAMAC electronics by VME modules.

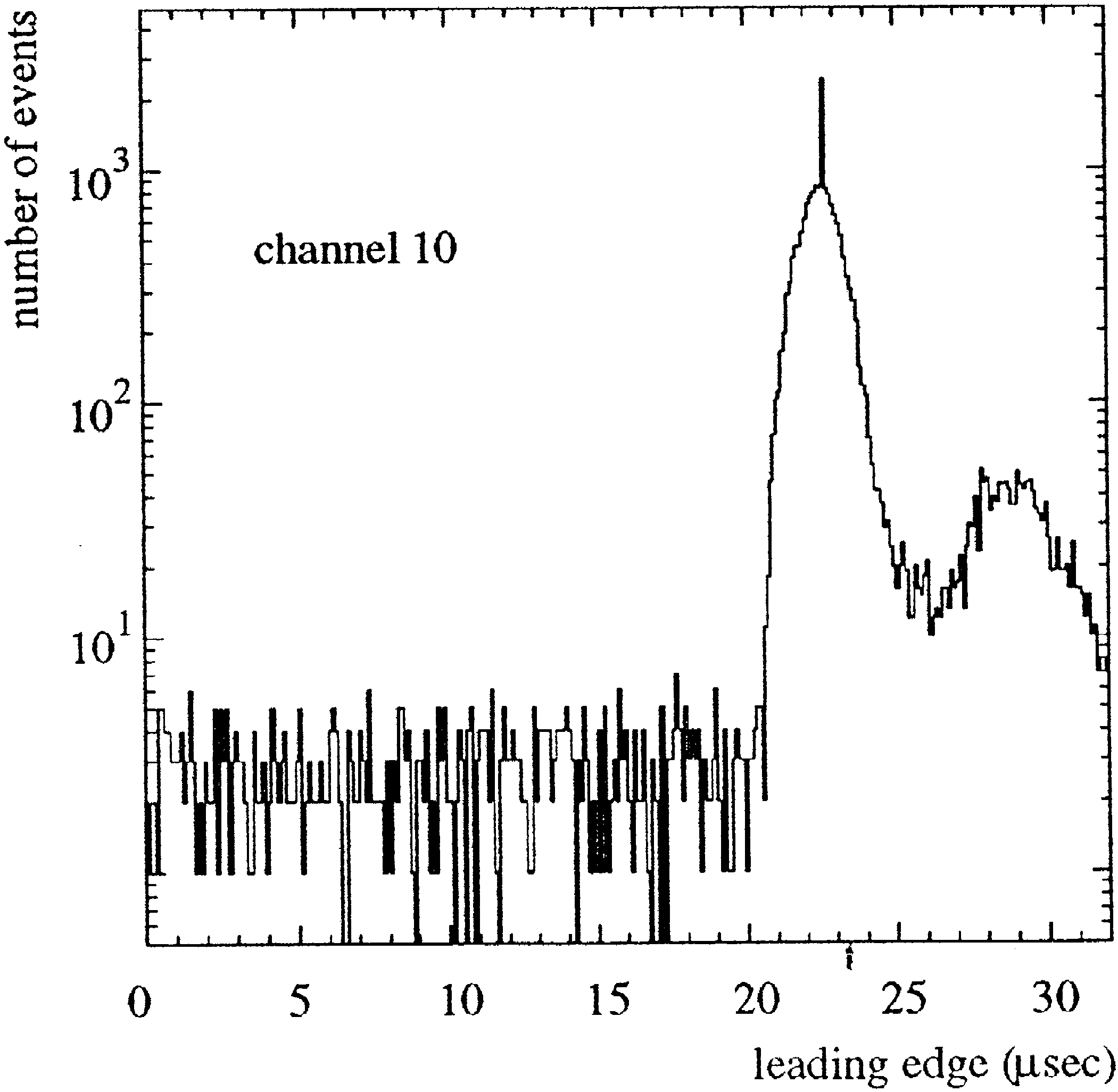
Fig. 4 shows the distribution of the leadingedge

times of one PMT for data taken with the 8fold

majority trigger. The sharp peak at 23

sec is given

by the time when this PMT was the triggering one

i.e. the eighth within a 2

sec window. The flat

Fig. 4. Leading edge times of PMT

10 of AMANDAB4 for

data taken with an 8fold majority trigger.

part is due to noise hits and the bulge after the main

distribution to afterpulses about 6% .

4.4. Calibration light sources and ice properties

An essential ingredient to the operation of a detec

tor like AMANDA is the knowledge of the optical

properties of the ice, as well as a precise time

calibration of the detector. Various light calibration

sources have been deployed at different depths in

order to tackle these questions:

The YAG laser calibration system

. It uses optical

fibers with diffusers located at each PMT. This

system is similar to that used for AMANDAA.

The range of transmittable wavelength is

450

nm, the time resolution is about 15 nsec at 530

nm, the maximum intensity emitted by the dif

fusers is 10

photons

pulse. Apart from ice in

vestigations, the laser system is used for time

calibration of the PMT closest to the diffuser and

for position calibration see Section 5 .

A nitrogen laser

at 1850 m depth, wavelength

337 nm, pulse duration 1 nsec, with a maximum

intensity of 10

photons

pulse.

Three DC halogen lamps

one broadband and two

with filters for 350 and 380 nm , maximum inten

sity 10 UVfiltered and 10 broadband pho

tons

second.

LED beacons

, operated in pulsed mode 500 Hz,

pulse duration 7 nsec, 10 photons

pulse and

14 15

DC mode 10 to 10 photons

sec , wave

length 450 nm. A filter restricts the output of a

few beacons at 390 nm, with reduced intensity.

()

E. Andres et al.

Astroparticle Physics 13 2000 1–20

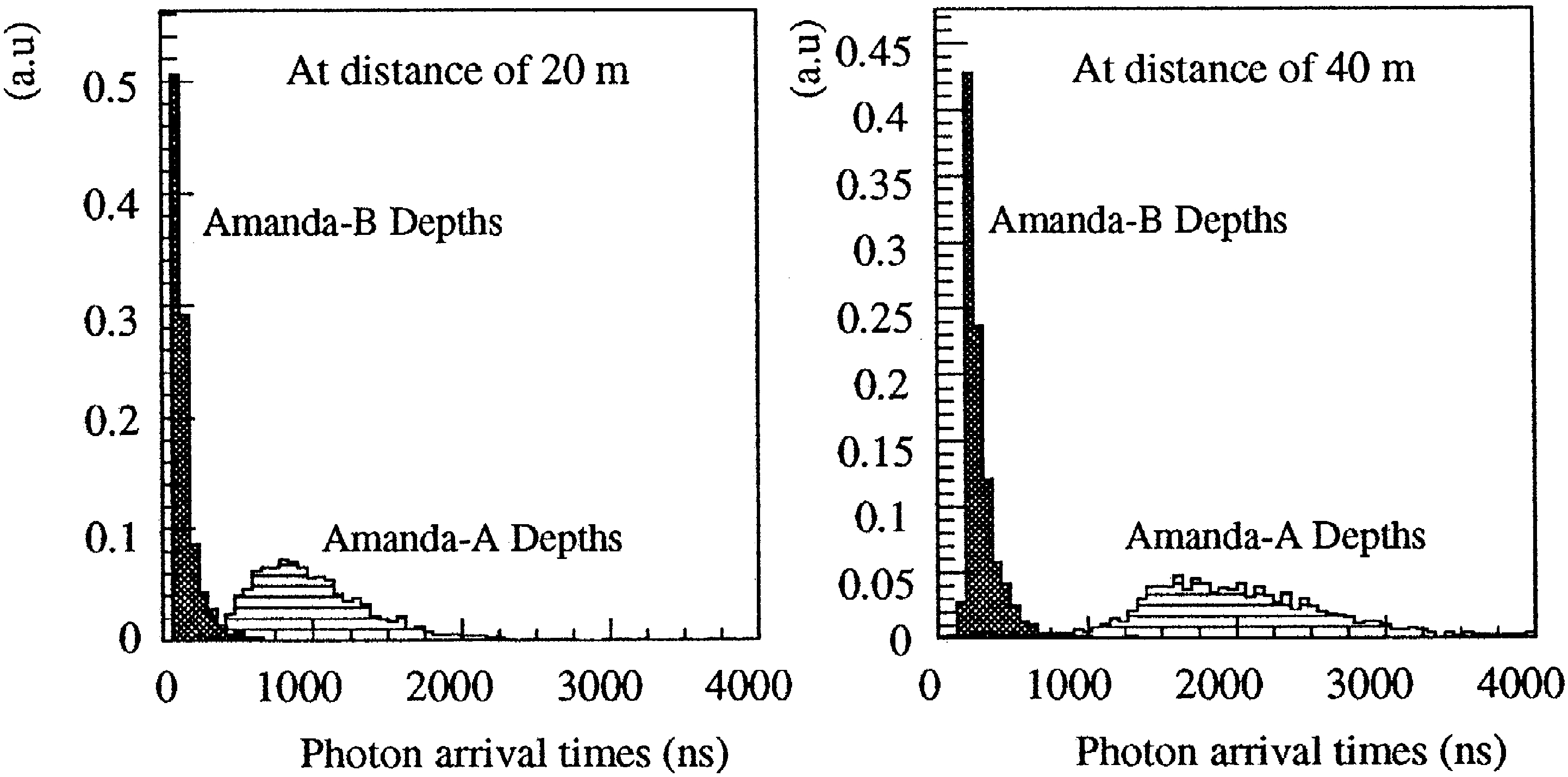
Fig. 5. Arrival time distributions for 510 nm photons for two

sourcedetector distances. Black histograms: AMANDAB.

Hatched histograms: AMANDAA. The histograms are normal

ized to the same area.

Timeofflight measurements have been made for

a large variety of combinations of optical fiber emit

ters and PMTs for the YAG laser system, and at

different wavelengths and intensities. The nitrogen

laser provided data at 337 nm. The result is a

considerable database of hundreds of time distribu

tions. The width of the distributions is sensitive

predominantly to scattering and the tail to absorption

see 30 for details . The DC sources provide data

for attenuation, i.e. the combined effect of absorption

and scattering.

The YAG laser results indicate a dramatic im

provement compared to AMANDAA results. Fig. 5

shows the distributions of arrival time for sourcede

tector distances of 20 and 40 m, respectively, for

AMANDAA as well as AMANDAB depths. The

much smaller widths for AMANDAB support the

expectation that bubbles as the dominant source of

scattering have mostly disappeared at depths be

tween 1550 and 1900 m 16 .

Details of the analysis of the optical properties of

the ice at AMANDAB4 depths have been published

elsewhere 19 . Final results will be published in a

separate paper. The preliminary results can be sum

marized as follows: The absorption length

ab s

about 95 m for wavelengths between 337 and 480

nm and decreases to 45–50 m at 510 nm. The

effective scattering length

is about 24 m. The

eff

attenuation length

which characterizes the de

att

crease of the photon flux as a function of the dis

tance is about 27 m. These values are averages over

the full depth interval covered by AMANDAB4.

The variation of attenuation over this depth range is

within

30%.

5. Calibration of time response and geometry

5.1. Time calibration

The measured arrival times from each PMT have

to be corrected for the time offset

, that is, the time

it takes a signal to propagate through the PMT and

the coaxial cable and get digitized by the DAQ. The

time offset is determined by sending light pulses

from the YAG laser to the diffuser nylon balls

located below each OM. Two fibers are available for

each PMT, one single and one multimodal. The

time it takes for light to travel though the fiber is

measured using an OTDR Optical Time Domain

Reflectometer and subtracted from the time distribu

tions recorded.

For each PMT, the time difference between the

laser pulse at the surface and the PMT response

arriving back is measured. Upon arrival at the sur

face, the pulses have traveled through nearly 2000

meters of cable and are dispersed, with typical time

overthresholds of 550 nsec and rise times of 180

nsec. The threshold used for TDC measurements is

set to a constant value with the consequence that

small pulses will reach that value later than larger

ones. This causes an amplitudedependent offset or

‘‘time walk’’, which can be corrected for by

’

ADC . 1

true LE 0

Here,

is the measured leading edge time and

the true time at which the light pulse reaches the

true

photocathode. The estimates of the time offset

and

the timewalk term

are extracted from scatterplots

like the one shown in Fig. 6.

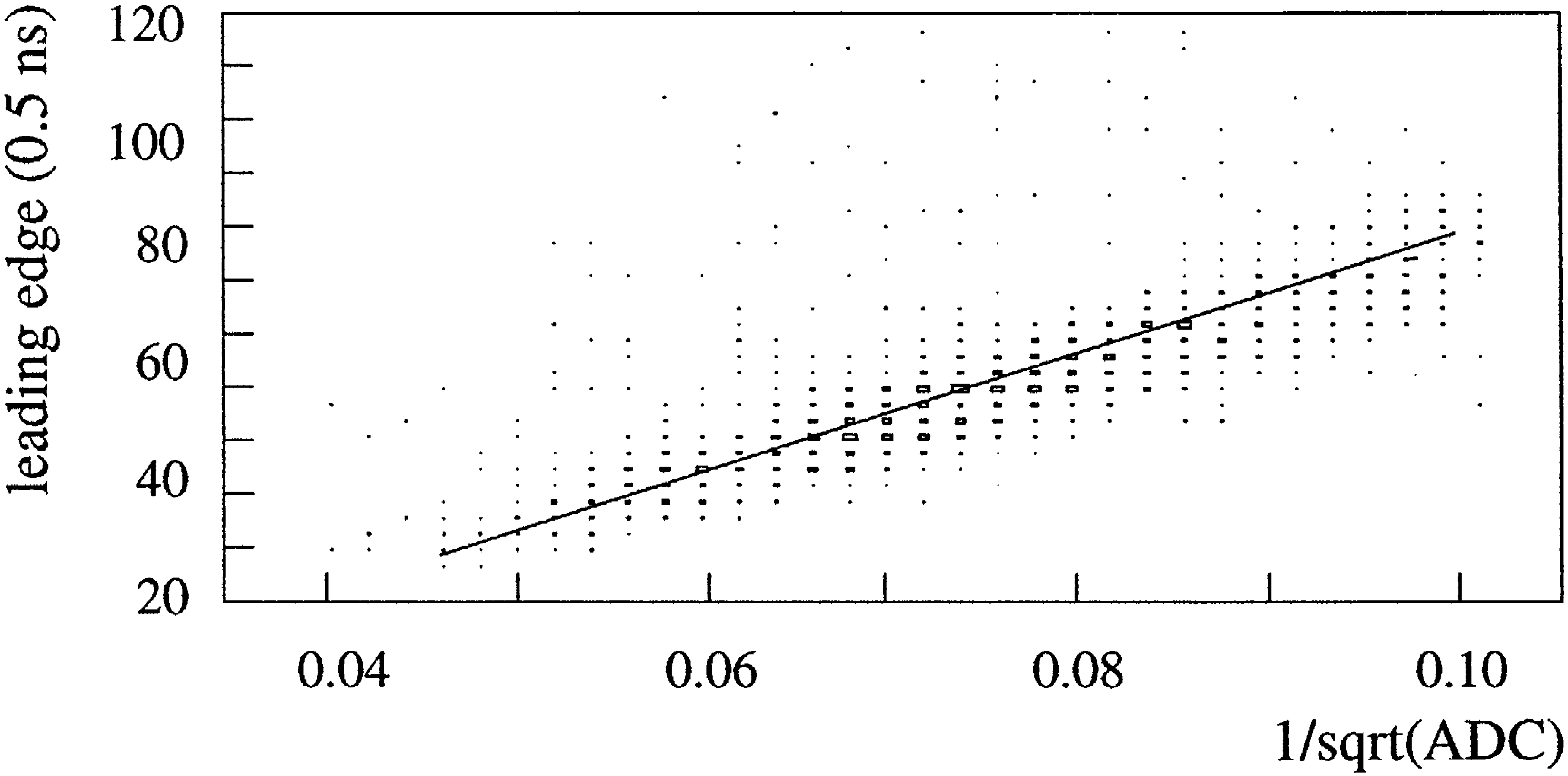
The time resolution achieved in this way can be

estimated by the standard deviation of a Gaussian fit

Fig. 6. Example of a fitted leading edge with 100

ADC

1200

for module 19 on string 3. The ADC value measures the peak

value of the amplitude.

()

E. Andres et al.

Astroparticle Physics 13 2000 1–20

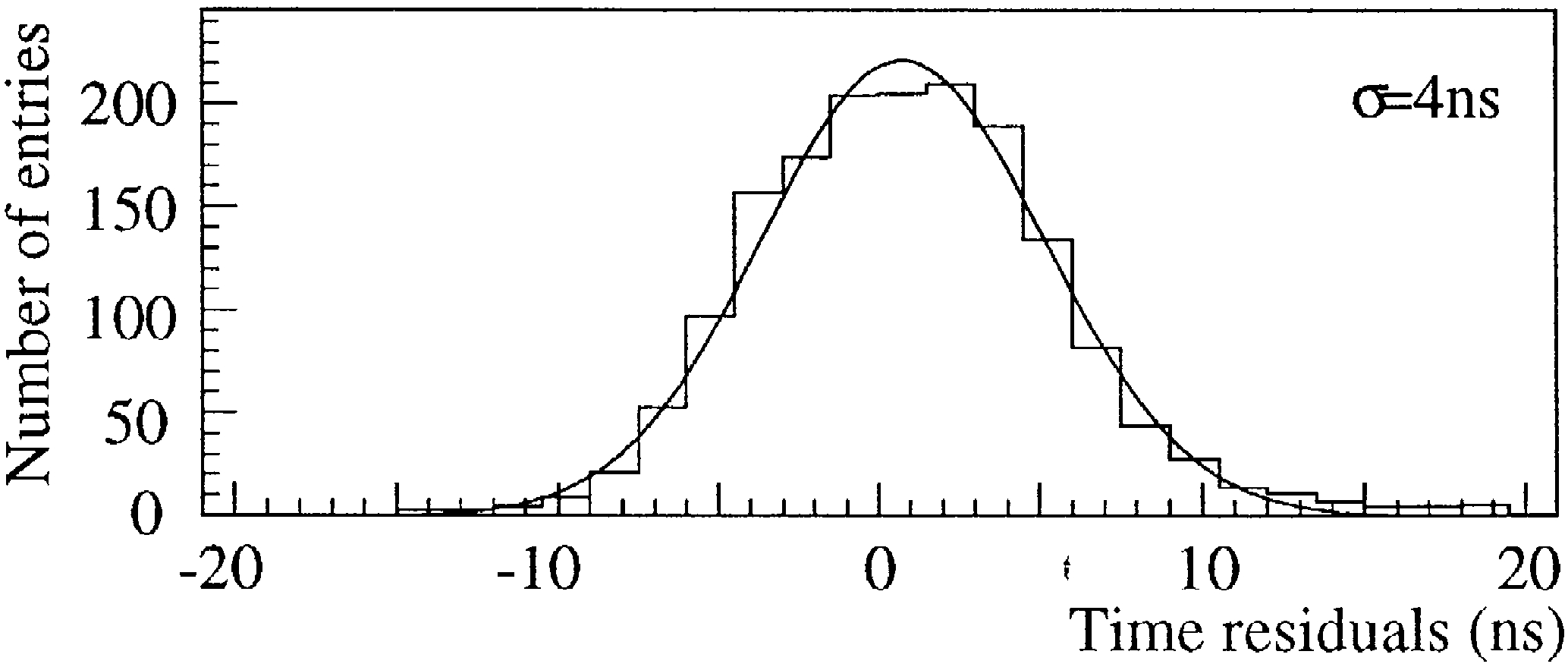
to the distribution of time residuals after correction,

yielding 4–7 nsec see Fig. 7 for an OM with 4 nsec

resolution . Part of the variation is due to quality

variations of the 1996 optical fibers. Laboratory

measurements yield a Gaussian width of 3.5 nsec

after 2 km cable.

5.2. Position calibration

Information about the exact geometry of the array

can be obtained by different methods. Firstly, the

measured propagation times of photons between dif

ferent light emitters and receivers can be used to

determine their relative positions. Secondly, absolute

positions can be obtained from drill recordings and

pressure sensors.

5.2.1. Laser calibration

The YAG laser, the nitrogen laser and the pulsed

LEDs can be used to infer the OM positions from the

timeofflight of photons between these light sources

and the OMs. The zero time is determined from the

response of the OM closest to the light source which

is triggered by unscattered photons. This PMT is

lowered in voltage in order not to be driven in

saturation, and a time correction accounting for the

longer PMT transit time is added. In contrast to the

close OM, the distant OMs see mostly scattered

photons. However, for a few of the events out of a

series of about 1500 laser pulses, the leading edge

should be produced by photons which are only

slightly scattered. Therefore, the distance between

emitter and OM can be estimated from the earliest

events in the timedifference distribution see Fig. 8 .

In order to reduce the sensitivity to fluctuations in

the number of early hits and binning effects, the

whole left flank of the distribution is fitted with a

Fig. 7. Residuals after subtracting the time correction obtained

with the fitted parameters

and

for module 19 on string 3.

The standard deviation of the Gaussian fit is 4 nsec.

Fig. 8. Simulated timeshift distribution for 1500 onephoto

electron events, for a distance of 60 m between emitter and

receiver. A Gaussian smearing of 10 nsec was applied to individ

ual entries. Clear ice would yield a 10 nsec wide peak at 0 nsec.

Gaussian between the maximum of the distribution

height0 in Fig. 8 and the first bin with a height

larger than

height1=1/1

–

height

–

. The cor

rected ‘‘first’’ time is given by that bin

bin1

for

which the fitted Gaussian yields a height exceeding

height1

. This time has to be corrected further for

the shifts due to scattering which are expected even

for the first bin of the distribution. The corrections

were obtained from Monte Carlo MC calculations

and are almost insensitive to variations in absorption

and scattering length of a few meters.

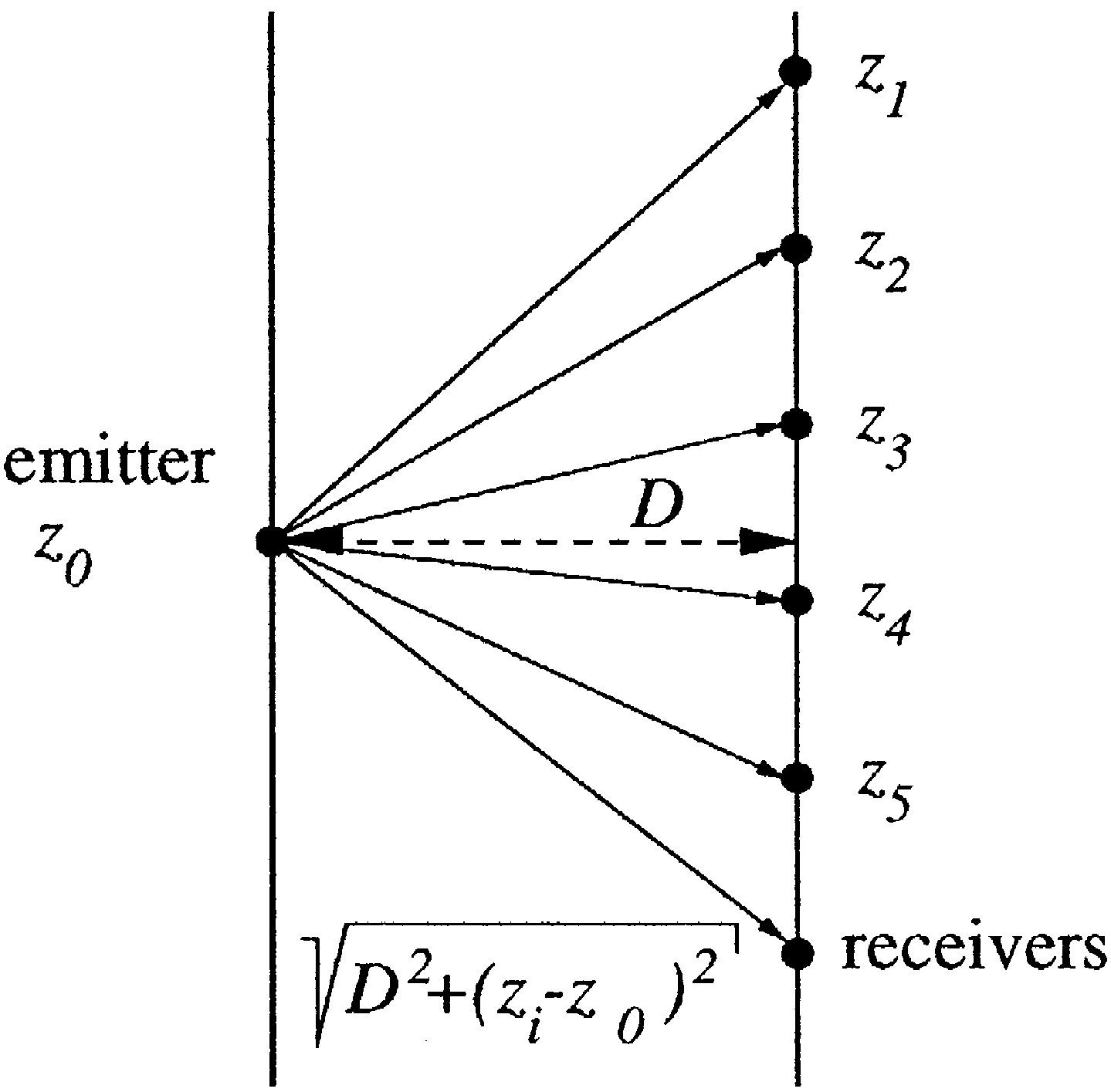
Given the limited number of measured emitterOM

combinations available for AMANDAB4, it would

have been impossible to keep the coordinates of each

OM as free parameters in a global position fit.

Therefore, all strings were assumed to be straight

and parallel and the OMs to be at a fixed vertical

distance 20 m relative to each other. For each

emitter covering enough OMs, a graph of the dis

tance

between source and OM

versus depth

can be drawn see Fig. 9 . The interstring dis

Fig. 9. Principle of position measurement.

()

E. Andres et al.

Astroparticle Physics 13 2000 1–20

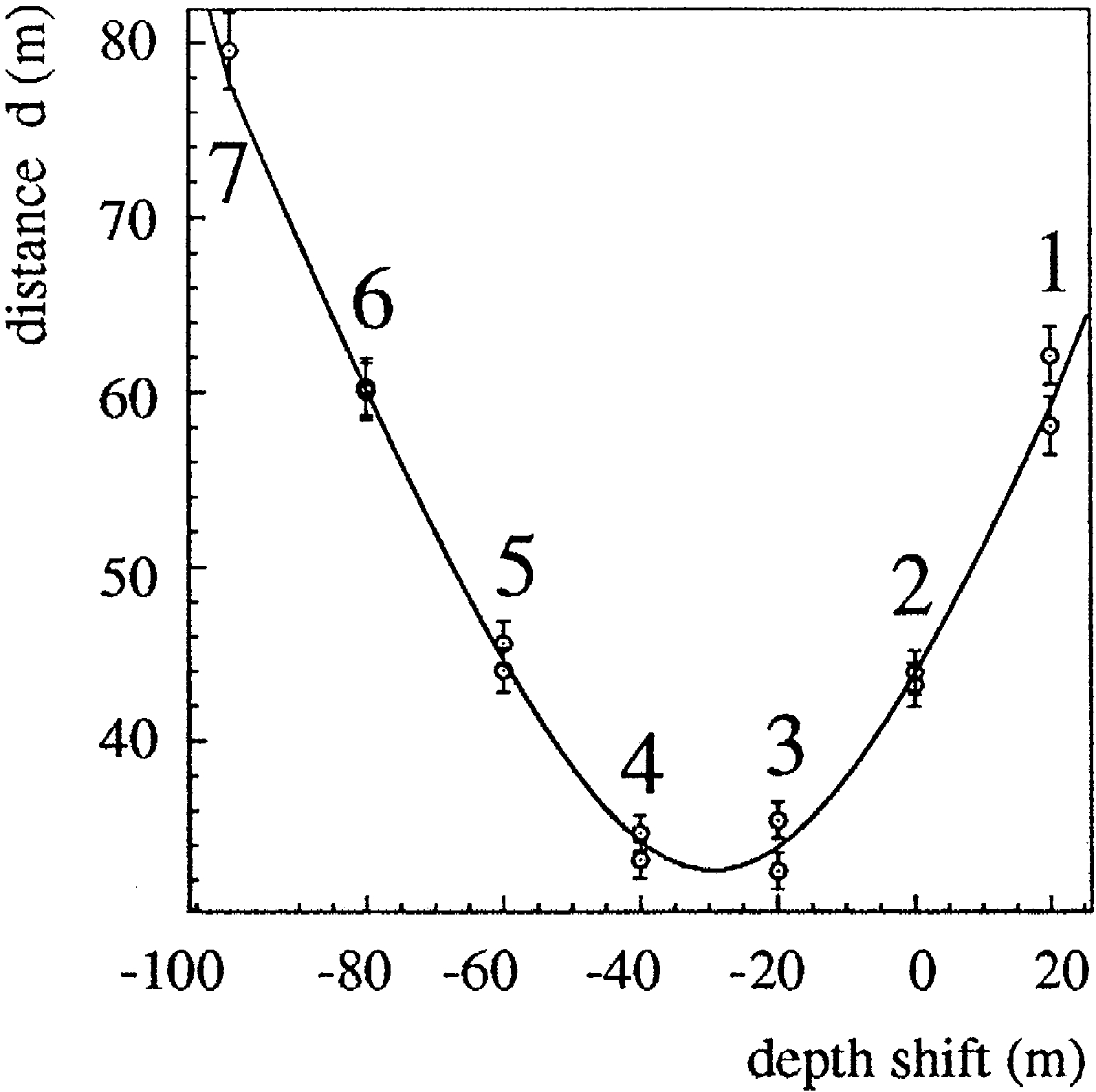
Fig. 10. Fit of the distance

versus depthshift

tween OMs at string 4 and a laser emitter at string 2. String

distance

and depth shift

are given by the minimum of

the parabola.

tance

and emitter depth

with respect to the

can be estimated from this graph by fitting Fig. 10

(

. . .

The residuals from all fits to the 1996 AMANDA

B4 data have a standard deviation of 2 m.

In 1996–1997, six more strings were added on the

outside of the B4 detector, and a new position cali

bration performed. The increased statistics and possi

bilities of new crosschecks and constraints enabled

correction of the existing geometry with an uncer

tainty of 1 m in the horizontal plane and 0.5–1.0 m

in depth.

5.2.2. Drill data

The geometry of the array is surveyed in an

independent way by monitoring the position of the

drillhead while it is going down each hole. The data

were recorded by the drill instrumentation at each 10

cm step, recording the pathlength, the value of the

Earth’s magnetic field as measured by a flux magne

tometer and the angles bank and elevation given by

perpendicular pendulums. This information can then

be used to reconstruct the hole profiles. The results

found are compatible with the laser measurements

within 1–2 m in the horizontal plane. The advantage

of this method is that it yields positions relative to

the surface, i.e. in a global reference frame. It also

takes into account tilts in the strings. However, it

does not yield the depth locations of the OMs. The

absolute depths of the strings were given by pressure

sensors deployed with the OMs.

6. Simulation and reconstruction of muons

6.1. Simulation

Downgoing muons are generated by full atmo

spheric shower programs which simulate the produc

tion of muons by isotropic primary protons 20 or

protons and nuclei 21 with energies up to 1 PeV.

The muons are propagated down to a plane close to

the detector. Upgoing muons are generated from

atmospheric neutrinos, using the flux parameteriza

tion given in Ref. 22 , from neutralinos annihilating

in the center of the Earth, using the flux calculations

of 2,3 , and from point sources, using arbitrary

energy distributions and source angles; they may

start anywhere within the fiducial volume which

increases with increasing neutrino energy due to the

muon range and are propagated simulating the full

stochastic energy loss according to 23 .

It would be computationally impractical to gener

ate and follow the path of each of the multiply

scattered Cherenkov photons produced by muons

and secondary cascades for every simulated event.

Therefore, this step is accomplished by doing the

photon propagation only once by a separate MC

program and storing the results in large multidimen

sional tables. The tables give the distribution of the

mean number of photoelectrons expected and of the

time delay distribution, as a function of the position

and the orientation of a PMT relative to the muon

track. They include the effects of the wavelength

dependent quantum efficiency, the transmission coef

ficients of glass spheres and optical gel, and the

absorption and scattering properties of the ice. Once

the tables are compiled, events can be simulated

quickly by locating the PMT relative to any input

particle and looking up the expected number and

time distribution of photoelectrons in the tables

. The

known characteristics of the AMANDA PMTs, the

measured pulse shapes, pulse heights and delays

after signal propagation along the cables, and the

This method assumes that ice is isotropic and homogeneous

which is reasonable in a first approximation: firstly, since the

variations of the original ice with depth have been measured to be

smaller than

25%, secondly, since the freshly frozen ice in the

holes occupies only a small volume of the array.

()

E. Andres et al.

Astroparticle Physics 13 2000 1–20

effect of electronics are then used to generate ampli

tude and time information 24 .

6.2. Reconstruction

The reconstruction procedure for a muon track

consists of five steps:

1. Rejection of noise hits, i.e. hits which have either

a very small ADC value or which are isolated in

time with respect to the trigger time or with

respect to the nearest hit OM.

2. A line approximation following 25 which yields

a point on the track,

, and a velocity

: : :

ii i i

: :

with

and

being the coordinate vector and

response time of the

th PMT.

3. A likelihood fit based on the measured times

which takes the track parameters obtained from

the line fit as start values. This ‘‘time fit’’ yields

angles and coordinates of the track as well as a

likelihood

time

4. A likelihood fit using the fitted track parameters

from the time fit and varying the light emission

per unit length until the probabilities of the hit

PMTs to be hit and nonhit PMTs to be not hit are

maximized. This fit does not vary the direction of

the track but yields a likelihood

which can

hit

be used as a quality parameter.

5. A quality analysis, i.e. application of cuts in order

to reject badly reconstructed events.

Steps 3 and 5 are outlined in the following two

subsections.

6.3. Time fit

In an ideal medium without scattering, one would

reconstruct the path of minimum ionizing muons

most efficiently by a

minimization process. Due

to scattering in ice, the distribution of arrival times

of photoelectrons seen by a PMT is not Gaussian but

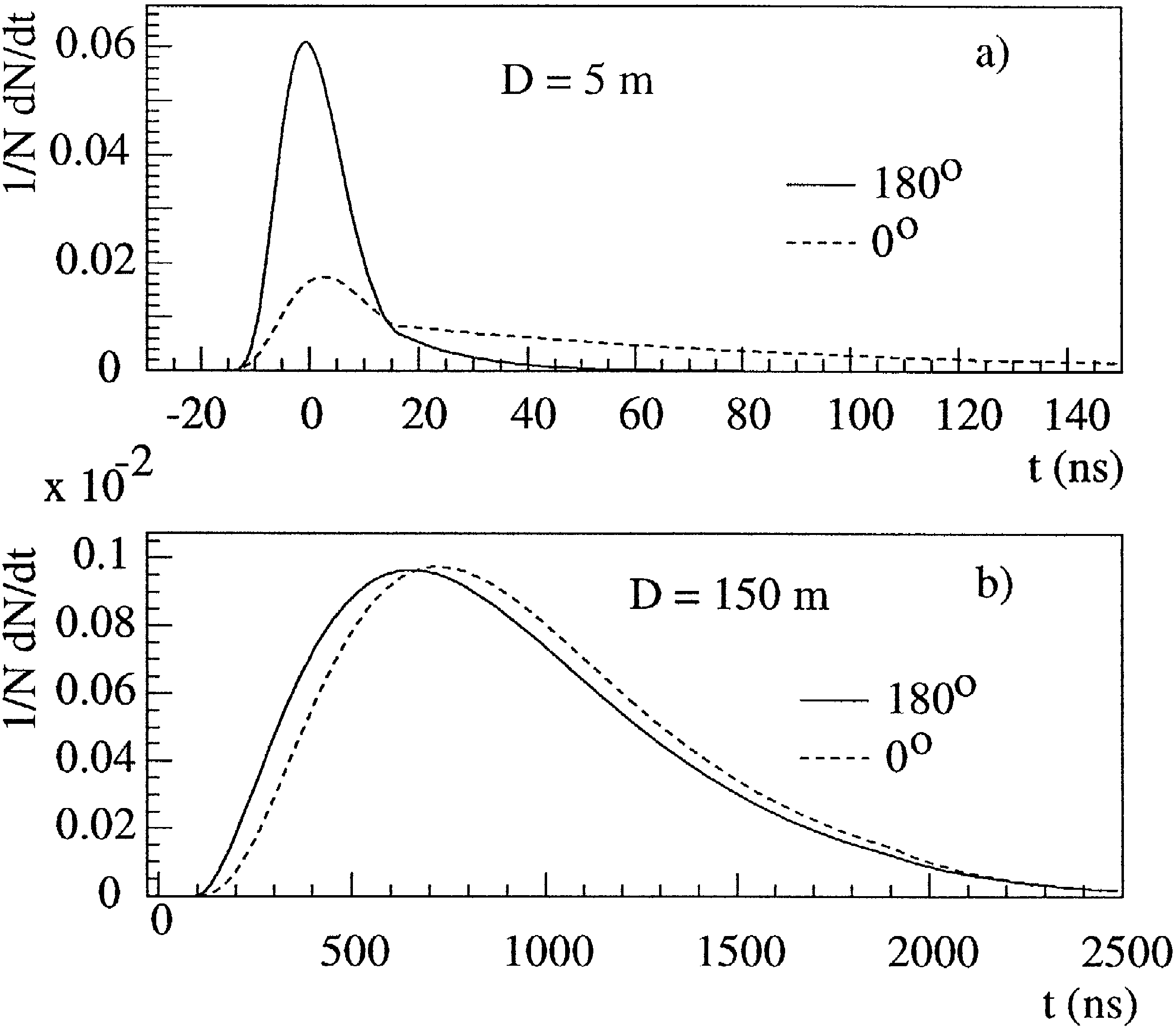
has a long tail at the high side – see Fig. 11.

To cope with the nonGaussian timing distribu

tions we used a likelihood analysis. In this approach,

a normalized probability distribution function

gives the probability of a certain time delay

for a

Fig. 11. Delaytime distributions for modules facing full curves

and backfacing dashed curves a muon track. Data are shown for

. .

muon tracks with impact parameters of a 5 meters and b 150

meters.

given hit

with respect to straightly propagating

photons. This probability function is derived from

the MC simulations based on the photon propagation

tables introduced in Section 6.1. The probability

depends on the distance and the orientation of the

PMT with respect to the muon track. By varying the

track parameters the logarithm of a likelihood func

tion

is maximized.

log

. .

all hits

In order to be used in the iteration process, the

time delays as obtained from the separate photon

propagation Monte Carlo have to be parameterized

by an analytic formula. The parameterization of the

propagation model itself is extended to allow for

timing errors of PMTs and electronics as well as the

probability of noise hits at random times. The

AMANDA collaboration has developed two inde

pendent reconstruction programs, which are based on

different parameterizations of the photon propagation

and different minimization methods 26,27,29 . The

comparison of these algorithms and the use of differ

ent optical models show that the results of both

methods are in good agreement with each other and

do not depend on a finetuning of the assumed

optical parameters. Fig. 11 shows the result of the

parameterization of the time delay for two distances

and for two angles between the PMT axis and the

muon direction. At a distance of 5 m and a PMT

()

E. Andres et al.

Astroparticle Physics 13 2000 1–20

facing toward the muon track, the delay curve is

dominated by the time jitter of the PMT. However, if

the PMT looks in the opposite direction, the contri

bution of scattered photon yields a long tail towards

large delays. At distances as large as 150 m, distribu

tions for both directions of the PMT are close to

each other since all photons reaching the PMT are

multiply scattered.

The parameterization used for most of the results

presented in this paper is a Gamma distribution

modified with an absorption term 28 ,

with the distance

between OM and muon track, the

scaled distance

0.8

sin

, the absorption

length

and only two parameters

7001 ns and

50 m.

The second approach uses an Fdistribution with

an exponential tail for large timedelays, which re

sults in a comparable accuracy 26 .

6.4. Quality analysis

Quality criteria are applied in order to select

events which are ‘‘well’’ reconstructed. The criteria

define cuts on topological event parameters and ob

servables derived from the reconstruction. Below we

list those used in the following:

Speed

of the line fit. Values close to the speed

of light indicate a reasonable pattern of the mea

sured times, values smaller than 0.1 m

nsec indi

cate an obscure time pattern.

‘‘Time’’ likelihood per hit PMT log

time hit

Summed hit probability for all hit PMTs

hit

‘‘Hit’’ likelihood normalized to all working chan

nels, log

hit all

The latter two parameters are good indicators of

whether the location of the fitted track, which

relies exclusively on the time information, is

compatible with the location of the hits and non

hits within the detector.

Number of direct hits,

, which is defined to be

dir

the number of hits with time residuals

mea

. .

sured

fit smaller than a certain cut value.

We use cut values of 15 nsec, 25 nsec and 75

nsec, and denote the corresponding parameters as

. . .

15 ,

25 and

75 , respectively. In

dir dir dir

creasing the time window leads to higher cut

values in

but allows a finer gradation of the

dir

cut.

Events with more than a certain minimum num

ber of direct hits i.e. only slightly delayed pho

tons are likely to be well reconstructed. This cut

turned out to be the most powerful cut of all 29 .

The projected length of direct hits onto the recon

structed track,

. A cut in this parameter rejects

dir

events with a small lever arm.

Vertical coordinate of the center of gravity,

COG

Cuts on this parameter are used to reject events

close to the borders of the array. Very distant

tracks are not likely to be well reconstructed.

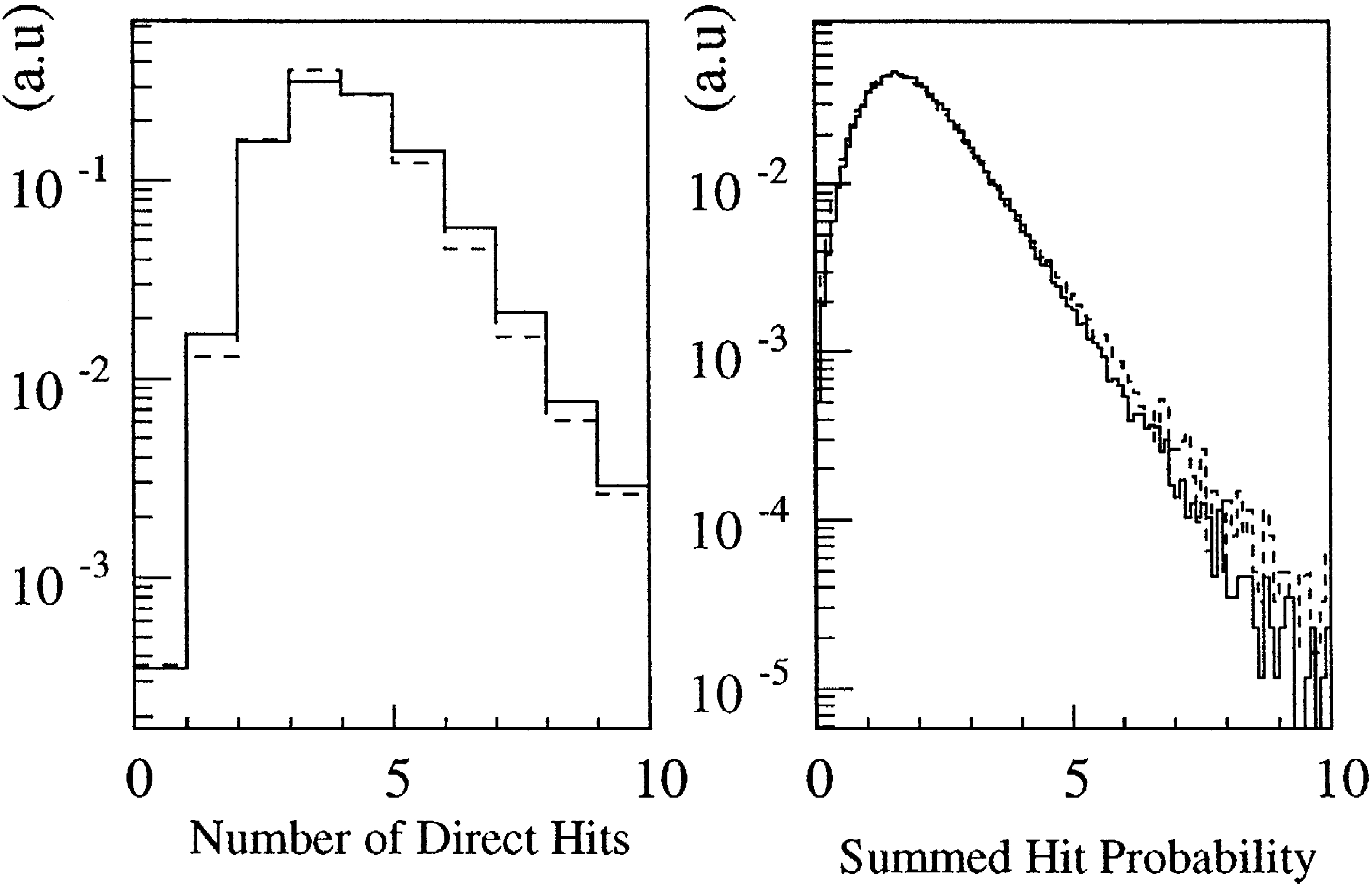
Fig. 12 shows the distribution of two of these

observables, the number of direct hits within 15

nsec,

15 , and the summed hit probability

dir hit

of all hit channels. It demonstrates the good agree

ment between results from MC and experiment.

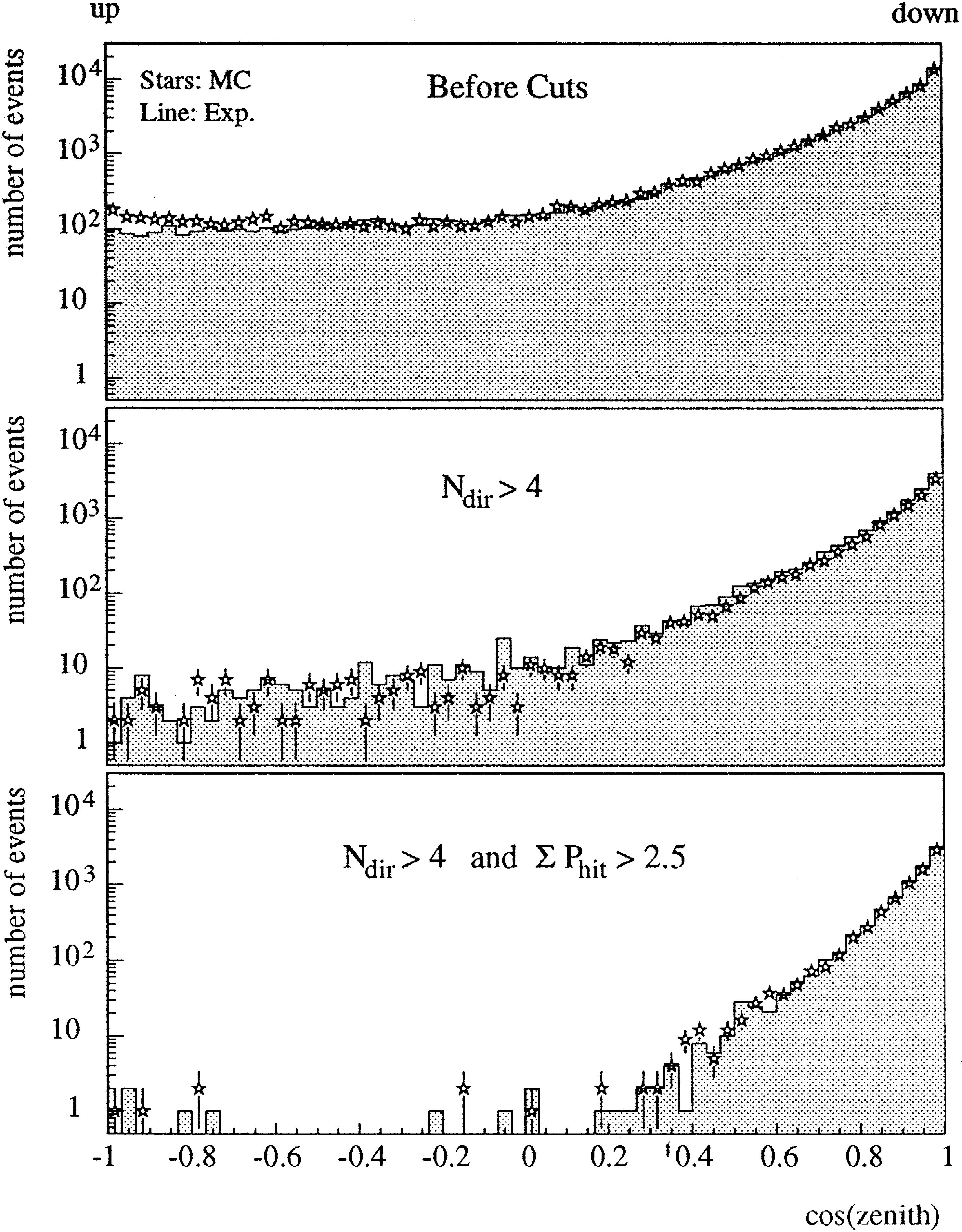
Fig. 13 demonstrates the effect of cuts on the

number of direct hits and the summed hit probability

on the reconstructed angular distribution of experi

mental data and the MC sample. The cuts are

5 and

2.5. Both samples are

direct hit

dominantly due to downgoing atmospheric muons.

Despite that, a small but similar fraction of events is

falsely reconstructed as upgoing events. After appli

cation of the above quality criteria the tail below the

horizon almost disappears. Note that not only the

Fig. 12. Distributions of two reconstructed event observables for

MC downgoing muon events dashed lines and from experimen

. .

tal data full lines . Left: Number of direct hits,

15 ; Right:

dir

summed hit probability,

hit

()

E. Andres et al.

Astroparticle Physics 13 2000 1–20

Fig. 13. Reconstructed zenith angle distributions of experimental

. .

data line and downward muon MC events points after a

stepwise application of quality cuts.

shapes but also the absolute passing rates on all cut

levels are in good agreement between data and Monte

Carlo. The angular mismatch between the recon

structed muon angle and the original angle used in

the MC simulation after both cuts is 5.5 degrees. We

note that this value strongly depends on the particu

lar set of cuts, the minimum acceptable passing rate,

the incident angle of the muon, and the range of

muons stopping in the array.

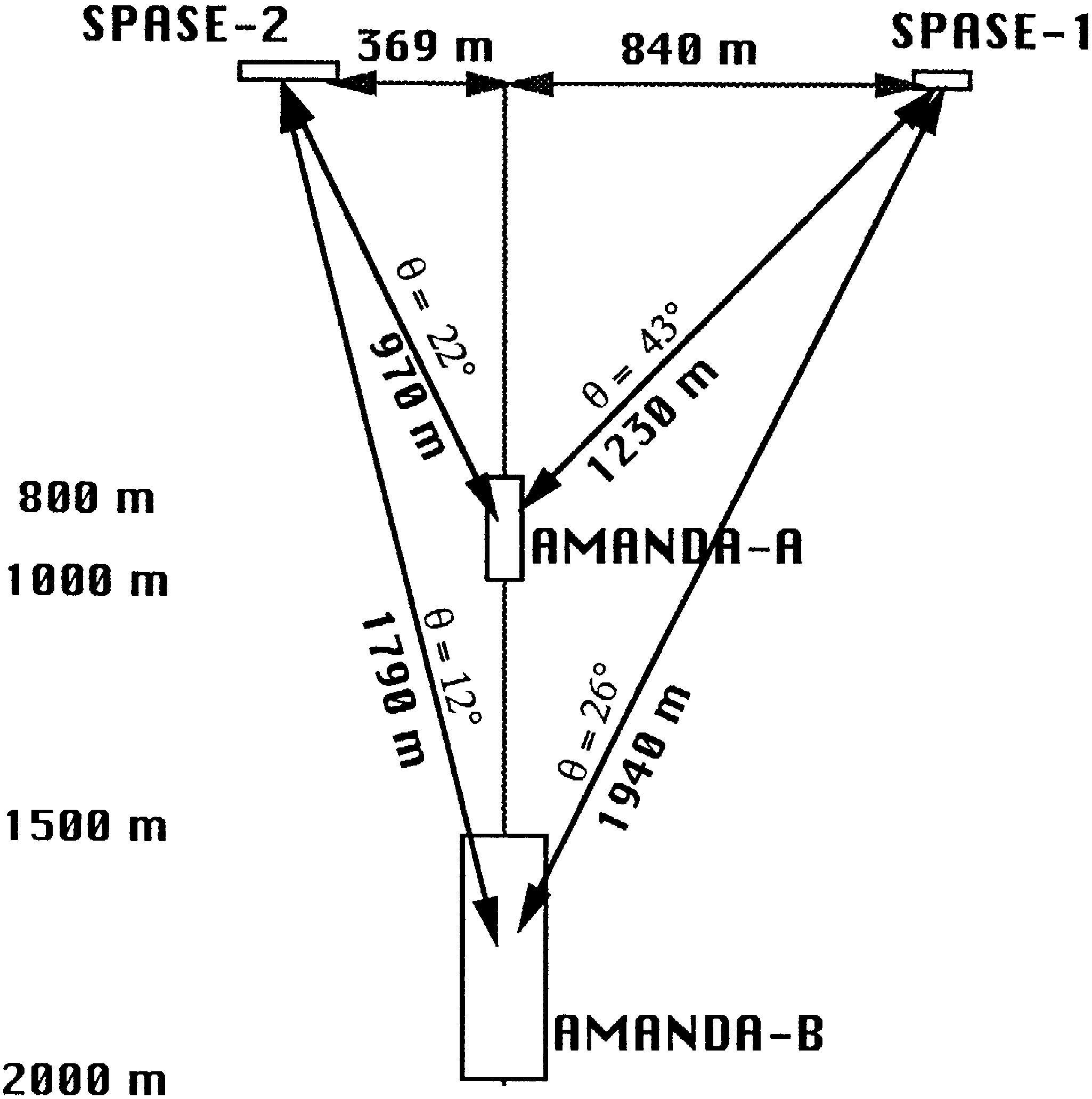
7. SPASE coincidences

AMANDA is unique in that it can be calibrated

by muons with known zenith and azimuth angles

which are tagged by air shower detectors at the

surface. AMANDAB4 has been running in coinci

dence with the two SPASE South Pole Air Shower

Experiment arrays, SPASE1 34 and SPASE2

35 . SPASE1 was located 840 m from the center of

the AMANDA array projected to the surface, whereas

SPASE2 is located 370 m away see Fig. 14 . The

scintillation detectors of SPASE2 are complemented

by an array of air Cherenkov detectors 31,32 . The

primary goal of these devices is the investigation of

the chemical composition of primary cosmic rays in

the region of the ‘‘knee’’ 33 . Another detector, the

gamma imaging telescope GASP, is also operated in

coincidence with AMANDA.

In this section, we summarize calibration results

obtained from the coincident operation of AMANDA

and SPASE2. SPASE2 consists of 30 scintillator

stations of 0.8 m

on a 30 m triangular grid. The

area of the array is 1.6

, and it has been

running since January 1996. For each air shower, the

direction, core location, shower size and GPS time

are determined. Showers with sufficient energy to

trigger SPASE2

100 TeV yield on average 1.2

muons penetrating to the depth of AMANDAB. On

every SPASE1 or SPASE2 trigger, a signal is sent

to trigger AMANDA. The GPS times of the separate

events are compared offline to match coincident

events.

A oneweek sample of these events has been

analyzed in order to compare the directions of muons

determined by AMANDAB4 to those of the show

ers measured by SPASE2. A histogram of the zenith

mismatch angle between SPASE2 and AMANDA

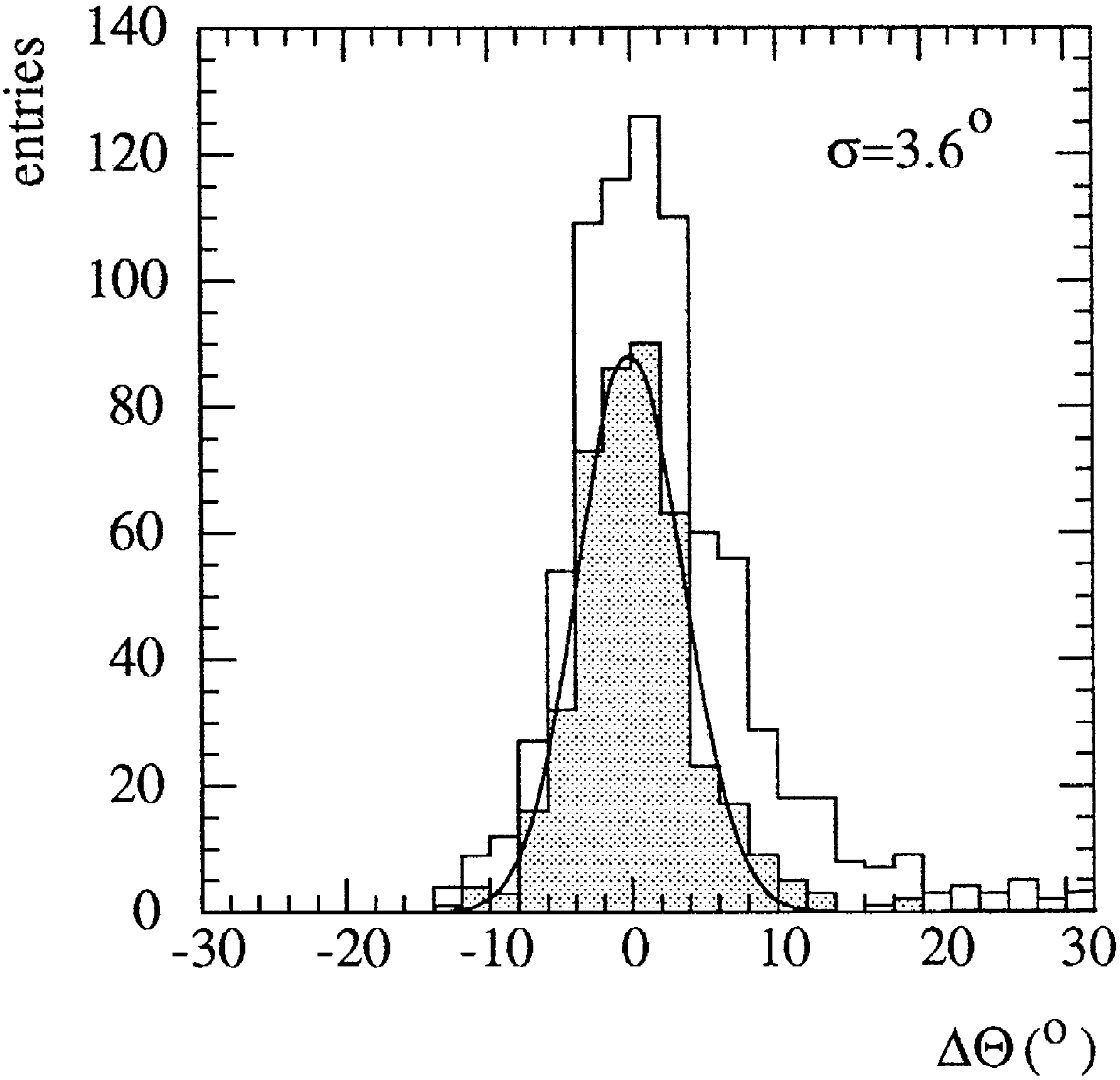
B4 is shown in Fig. 15. The selected events are

required to have

8 hits along 3 strings and to yield

a track which is closer than 150 m to the air shower

axis measured by SPASE2 upper histogram . The

hatched histogram shows the distribution of the zenith

Fig. 14. Side view of the two SPASE arrays relative to

AMANDAA and AMANDAB.

()

E. Andres et al.

Astroparticle Physics 13 2000 1–20

Fig. 15. Mismatch between zenith angles determined in

AMANDAB4 and SPASE2.

mismatch angle after application of the following

quality cuts:

likelihood log

)

12,

time hit

more than four hits with residuals smaller than 75

. .

nsec

)

dir

length of the projection of OMs with direct hits to

. .

the track larger than 50 meters

)

50 m .

dir

428 of the originally 840 selected events pass

these quality cuts. The Gaussian fit has a mean of

0.14

0.19 degrees and a width of

3.6

0.17 degrees. This is nearly 2 degrees better than

the resolution obtained in the previous section for

all

downward muons and for a different set of cuts. MC

yields a resolution of about 4 degrees.

The small mean implies that there is little system

atic error in zenith angle reconstruction. The SPASE

2 pointing accuracy, which contributes to the average

mismatch, depends on zenith angle and shower size.

For most of the coincidence events, the SPASE2

pointing resolution, defined as the angular distance

within which 63% of events are contained, is be

tween 1

and 2

31,32 .

8. Intensityvsdepth relation for atmospheric

muons

8.1. Angular dependence of the muon flux

In Section 6, the muon angular distribution was

shown as a function of various cuts in order to

demonstrate the agreement between experimental

data and MC simulations. In this section, we calcu

late the muon intensity

as a function of the zenith

angle

is given by

dead

DVe u

cut,

. .

rec

eff

where

is the number of muons assigned by the

analysis to a zenith angle interval centered around

cos

. For the analysis presented in this section,

we start from the angular distribution

rec

obtained from the reconstruction, without apply

ing cuts. This distribution is strongly smeared

see Fig. 13, top . We have calculated the ele

ments of the parent angular distribution

from the reconstructed distribution

using

rec

a regularized deconvolution procedure 36,37 .

is the runtime. We used the data from June 24,

1996, with

22.03 hours, and 9.86

events

triggering AMANDAB4.

corrects for the dead time of the data acqui

dead

sition system. This factor was determined from

the time difference distribution of subsequent

events. The deadtime losses for the two runs

used in this analysis are 12%, i.e.

0.88

dead

1.14.

is the solid angle covered by the correspond

ing cos

interval.

cut,

is the effective area, after the applica

eff

tion of a multiplicity trigger, for a given cut at

zenith angle

. The effective area is shown in

Fig. 16 as a function of the zenith angle and for

different cuts on the number of hit OMs.

is the reconstruction efficiency for zenith

rec

angle

which ranges between 0.82 at cos

1.0

and 0.75 at cos

0.2.

is the mean muon multiplicity at angle

at the ‘‘trigger depth’’. The trigger depth

was

eff

defined as depth of

, the center of gravity in

the vertical coordinate

of all hit OMs. The

average

depends on the angle. It is highest

eff

for cos

between 0.4 and 0.8 about 30 m below

the detector center and falls toward the vertical

at maximum 80 m below the center . The mean

muon multiplicity is about 1.2 for vertical tracks

and decreases towards the horizon. Since the

generator used in this analysis 20 simulates only

()

E. Andres et al.

Astroparticle Physics 13 2000 1–20

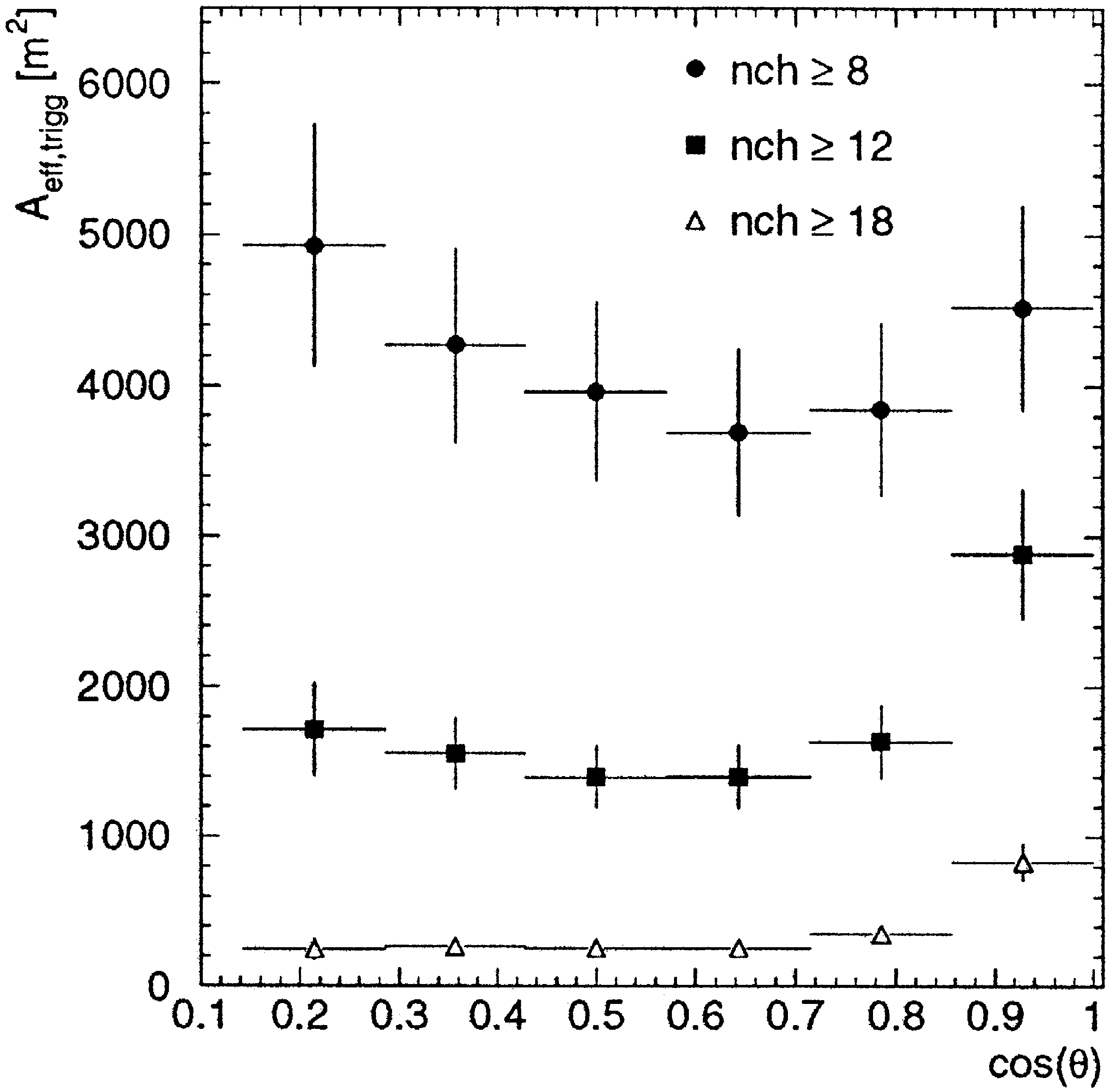
Fig. 16. Effective trigger area of AMANDAB4 as a function of

zenith angle, for 3 different majority criteria.

proton induced showers, this value is an underes

timation by about 10%.

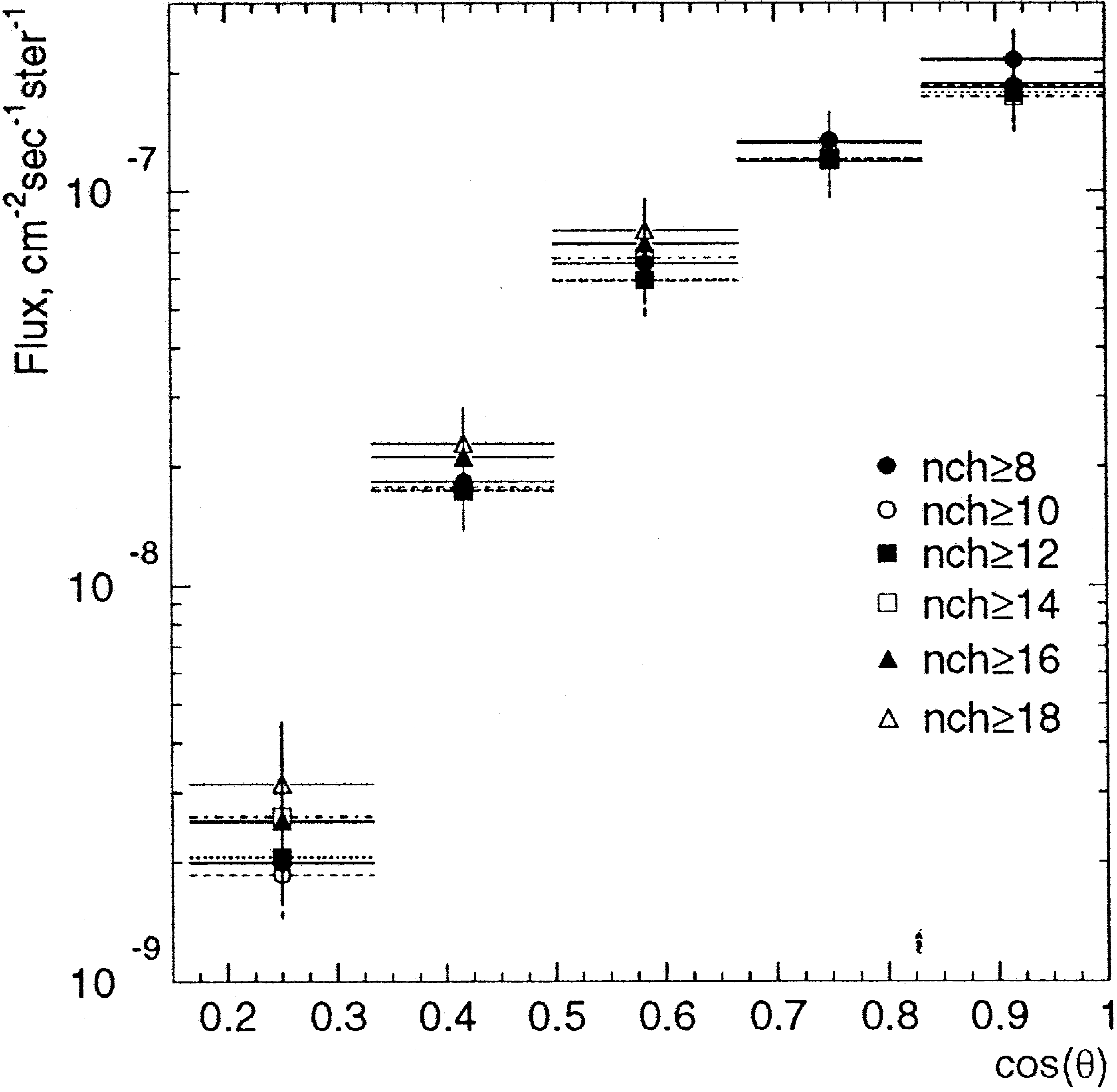
Fig. 17 shows the angular distribution of the flux

of downgoing muons,

, as obtained from Eq.

3 . In order to illustrate the stability of the method

with respect to cuts biasing the measured angular

distribution, the flux is shown for samples defined by

different majority triggers

)

8, 10, 12, 14, 16,

hit

18 . Apart from the point closest to the horizon

which is not only most strongly biased but also has

Fig. 17. Angular distribution of the downward going muon flux,

. .

, as obtained from Eq. 3 .

Fig. 18. Vertical intensity versus depth for AMANDA, BAIKAL

and DUMAND. The solid line gives the prediction of 38 which

coincides with the curves obtained from the parameterizations 5

and 6 .

the lowest statistics, deviations are within 25%. For

further studies we use the sample with

16.

hit

8.2. Transformation of angular flux to

ertical inten

sity as a function of depth

The measured flux

can be transformed into a

vertical flux

, where

is the ice thickness

seen under an angle

cos

. . . .

corr

The cos

conversion correcting for the sec

behavior of the muon flux is valid for angles up to

wx wx

46 . The term

taken from 44 corrects for

corr

larger angles and lies between 0.8 and 1.0 for the

angular and energy ranges considered here.

The vertical intensities obtained in this way are

plotted in Fig. 18 and compared to the depthinten

sity data published by DUMAND 45 and Baikal

wx w x

7 , and to the prediction by Bugaev et al. 38 . One

observes satisfying agreement of all experiments with

the prediction.

We also fitted our data to a parameterization

taken from 39,40 ,

0crit

eff

1. 5

eff

()

E. Andres et al.

Astroparticle Physics 13 2000 1–20

is the minimum energy necessary to reach

crit

the depth

. It is obtained from the parameterization

where

2 MeV

cm denotes the continuous energy loss due to

ionization, and

is proportional to the stochas

tic energy loss due to pair production, bremsstrahlung

and nuclear cascades. From this parameterization one

obtains

exp

is the nor

crit 0

malization parameter and

2.78 40 the spectral

index. We approximate

by an energy indepen

dent parameter

. Fitted to Eq. 5 , our data for the

eff

vertical intensity result in the following values for

and

eff

5.04

0.13 cm

ster

2.94

0.09

eff

This compares to

5.01

0.01 cm s

ster and

3.08

0.06 10 g cm ob

eff

tained for

8, showing that the result is rather

hit

insensitive to the actual cut condition.

For the purpose of completeness we give also the

results for the more usual parameterization,

e, 6

m m

wx wx

where

is set to 0 41 , to 2 42 or is a free

parameter 43 . The purely exponential dependence

0 clearly does not describe the data at depths

smaller than 4–5 km. Leaving all parameters free

43 , one obtains

0.89

0.30

10 cm

s ster ,

1453

612 g cm , and

2.0

0.25, being also in agreement with

fixed as in

Ref. 42 .

9. Search for upward going muons

AMANDAB4 was not intended to be a full

fledged neutrino detector, but instead a device which

demonstrates the feasibility of muon track recon

struction in Antarctic ice. The limited number of

optical modules and the small lever arms in all but

the vertical direction complicate the rejection of fake

events. In this section we demonstrate that in spite of

that the separation of a few upward muon candidates

was possible.

We present the results of two independent analy

ses. One uses the approximation of the likelihood

function by a Ffunction with an exponential tail

26 , the other the approximation by a Gamma func

tion with an absorption term 27 see Section 6.3 .

Both analyses apply separation criteria which are

obtained from a stepwise tightening of cuts on differ

ent parameters, in a way which improves the signal

tofake ratio given by the MC samples. Since the

MC generated samples of downwardgoing muons a

few million events run out of statistics after a

reduction factor of about 10

, further tightening of

cuts is performed without backgroundMC control

until the experimental sample reaches the same mag

nitude as the MC predicted signal.

For both analyses, the full experimental data set

of 1996, starting with Feb. 19th and ending with

Nov. 5th, was processed. It consists of 3.5

events.

9.1. Analysis 1

In a first step, a fast prefilter reduced this sample

to a more manageable size. It consists of a number of

cuts on quickly computable variables which either

correlate with the muon angle, or which to a certain

degree distinguish single muons from the downgoing

multimuon background events like, e.g. a cut on the

zenith angle from a line fit 25 , cuts on time differ

ences between OMs at different vertical positions,

and topological cuts requesting a minimum vertical

elongation of the event.

These cuts reduce the size of the experimental

data sample to 5.2%, the simulated atmospheric

muons to 4.8% and simulated upgoing events to

49.8%.

Simulated upgoing events and experimental data

have been reduced by further cuts,

At least 2 strings have to be hit this condition

relaxes the standard condition ‘‘

3 strings’’ and

increases the effective area in the vertical direc

tion .

The events were reconstructed below horizon, i.e.

)

log

)

time hit

0.15 m

nsec, where

is obtained from a fit

and

being the

coordi

ii i i

nates and times of the hit OMs.

()

E. Andres et al.

Astroparticle Physics 13 2000 1–20

Fig. 19. Number of events surviving prefilter and additional cuts

as a function of

15 . Solid line: 6month experimental data.

dir

dashed line: 6month expectation from atmospheric neutrinos.

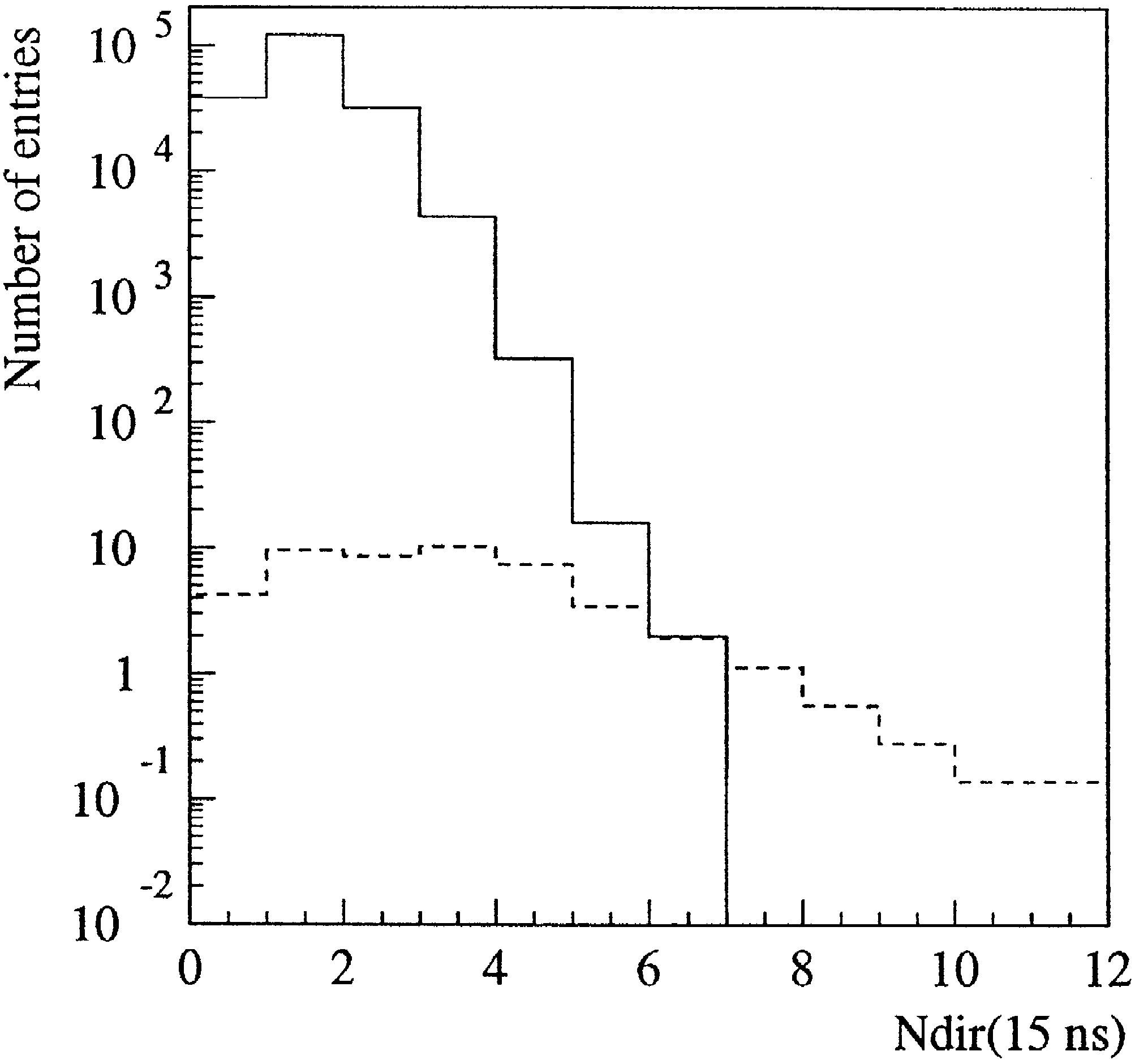
Fig. 19 shows the distribution of the number of

direct hits,

15 , of all events passing these cuts.

dir

The highest cut in

survived by

any

experi

direct

mental event is

6. The two surviving events

direct

are shown in Fig. 20. The Monte Carlo expectation

for upward muons from atmospheric neutrinos is 2.8

events, with an uncertainty of a factor 2, mostly due

to uncertainties in the sensitivity of the detector after

all cuts.

9.2. Analysis 2

The 3.5

experimental events were compared

to 3.5

MC events from atmospheric downgoing

muons which correspond to 2 days effective line

time. The MC data set for upward muons from

atmospheric neutrino interactions 47 consists of

2.5

events triggering AMANDAB4 – corre

sponding to 1.7 years effective live time.

In order to separate neutrino induced upward

muons, we applied a number of successively tight

ened cuts in the variables defined in Section 6.4.

This procedure reduced the experimental sample to

the expected signal sample after the following cuts:

1. reconstructed zenith angle

)

120

2. speed of the line fit 0.15

nsec,

. .

3. ‘‘time’’ likelihood log

)

time hit

i.e. normalizing to the degrees of freedom in

stead of the number of hit PMTs ,

. .

4. ‘‘hit’’ likelihood log

)

hit hit

5. number of direct hits for 25 nsec window,

dir

6. number of direct hits for 75 nsec window,

)

200 m,

dir

7. absolute value of the vertical coordinate of the

center of gravity

90 m with the center

COG

of the detector defining the origin of the coordi

nate system .

Three events of the experimental sample passed

these cuts, corresponding to a suppression factor of

8.9

. The passing rate for MC upward moving

muons from atmospheric neutrinos is 1.3% which

corresponds to 4.0 events in 156 days. The corre

sponding enrichment factor is 0.013

8.9

1.5

. One of the three experimental events was

Fig. 20. The two experimental events reconstructed as upward

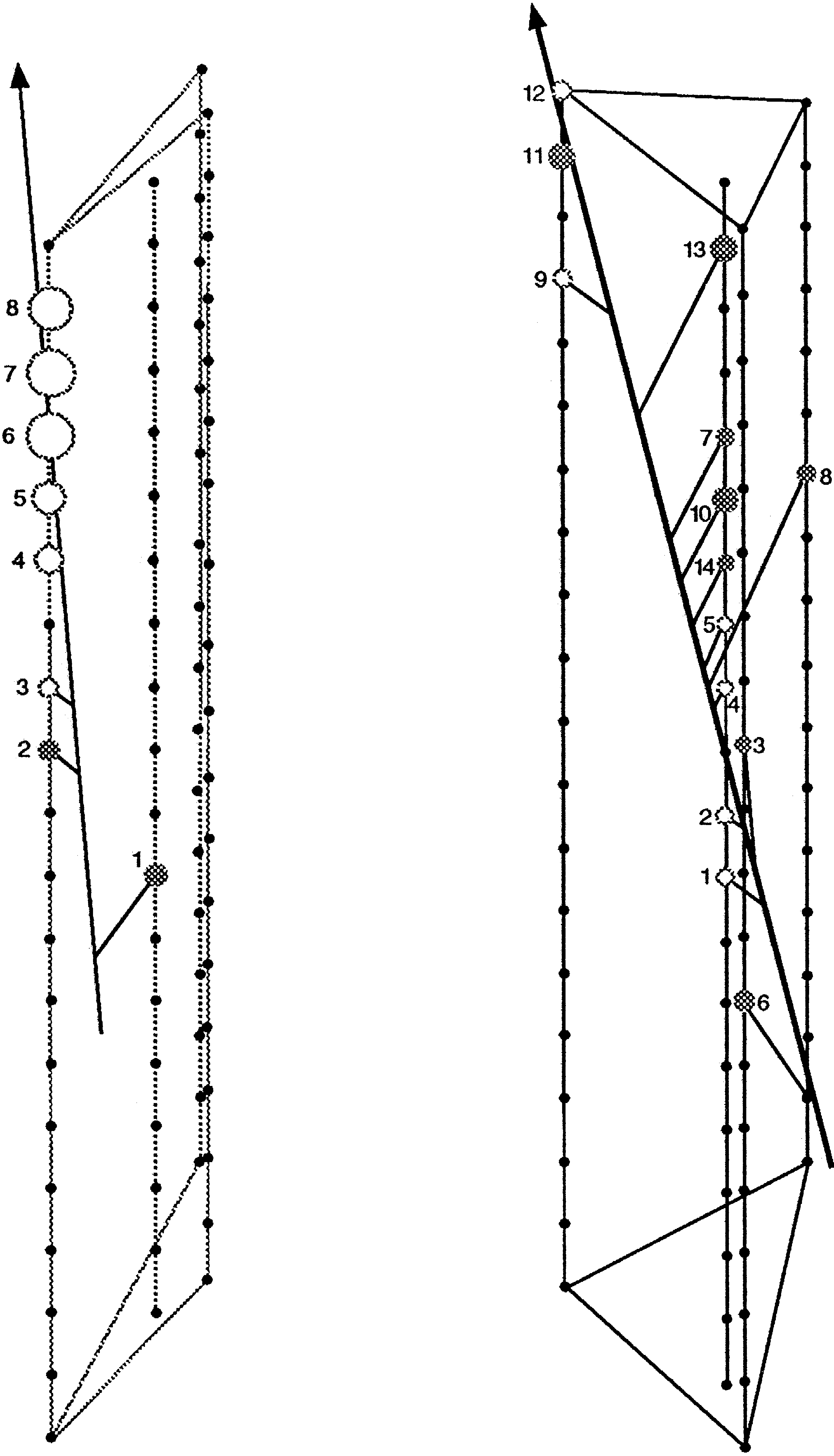
muons, left: ID 8427997, right: ID 4706870. The line with an

arrow symbolizes the fitted muon track, the lines from this track

to the OMs indicate light pathes. The amplitudes are proportional

to the size of the OMs. The numbering of the OMs refers to the

time order in which they are hit.

()

E. Andres et al.

Astroparticle Physics 13 2000 1–20

identified also in the search from the previous sub

section. A second event with

5 passes all cuts

dir

of the previous analysis, with the exception of the

cut.

dir

In order to check how well the parameter distribu

tions of the events agree with what one expects for

atmospheric neutrino interactions, and how well they

are separated from the rest of the experimental data,

we relaxed two cuts at a time retaining the rest and

inspected the distribution in the two ‘‘free’’ vari

ables.

Fig. 21 shows the distribution in

25 and

dir

75 . The three events passing

all

cuts are sepa

dir

rated from the bulk of the data. At the bottom of Fig.

21, the data are plotted versus a combined parameter,

. . .

20. In this parameter,

dir dir

. .

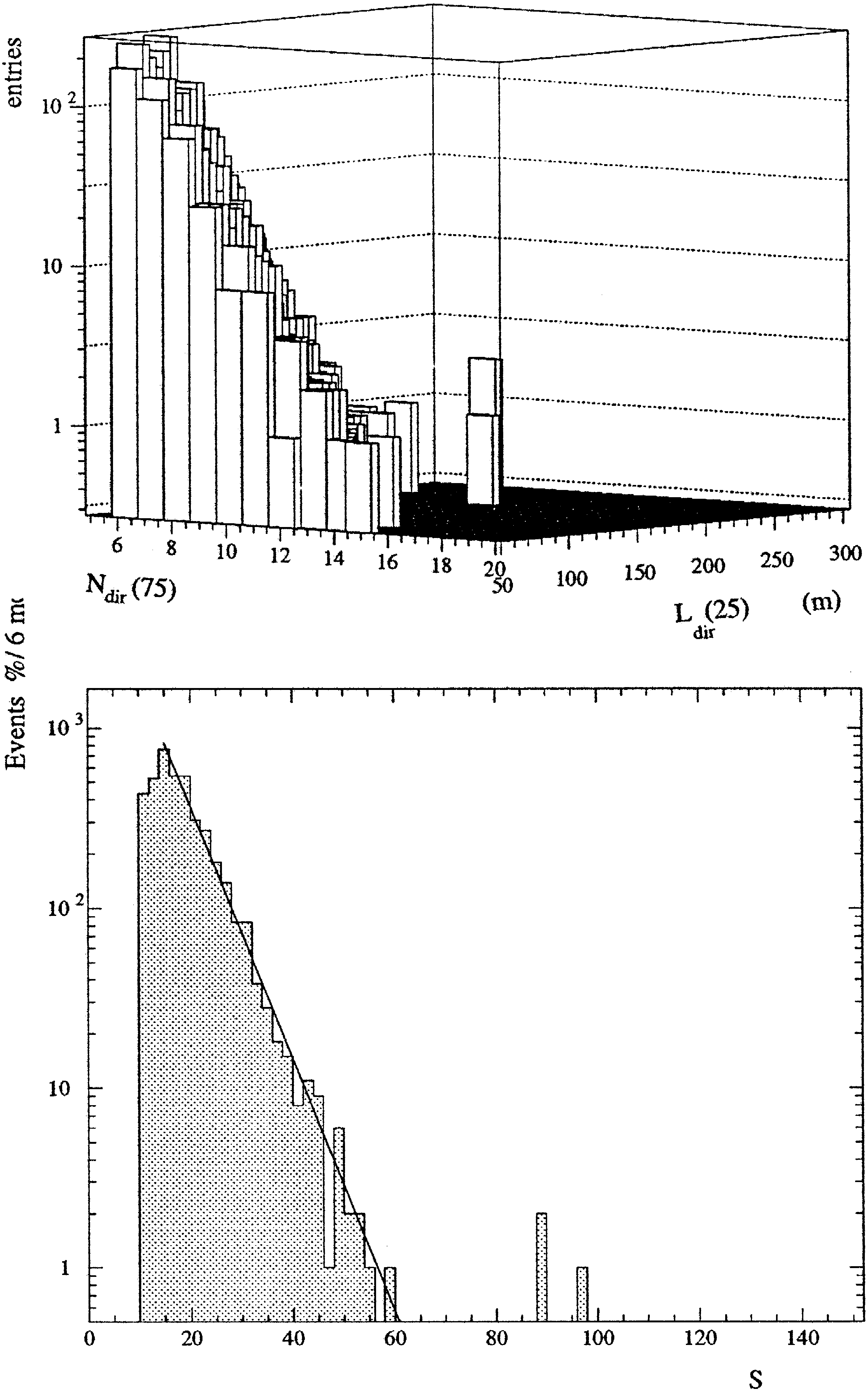
Fig. 21. Top – distribution in parameters

25 versus

75 ,

dir dir

bottom: distribution in the ‘‘combined’’ parameter

dir

20. The cuts applied to the event sample include all cuts

dir

with the exception of cuts 6 and 7.

Fig. 22. Distribution in parameters

versus

25 , after appli

dir

cation of all cuts with the exception of cuts 2 and 7, which have

been relaxed. top: experimental data, bottom: signal Monte Carlo

sample.

the data exhibit a nearly exponential decrease. As

suming the decrease of the background dominated

events to continue at higher

values, one can calcu

late the probability that the separated events are fake

events. The probability to observe one event at

70 is 15%, the probability to observe 3 events is only

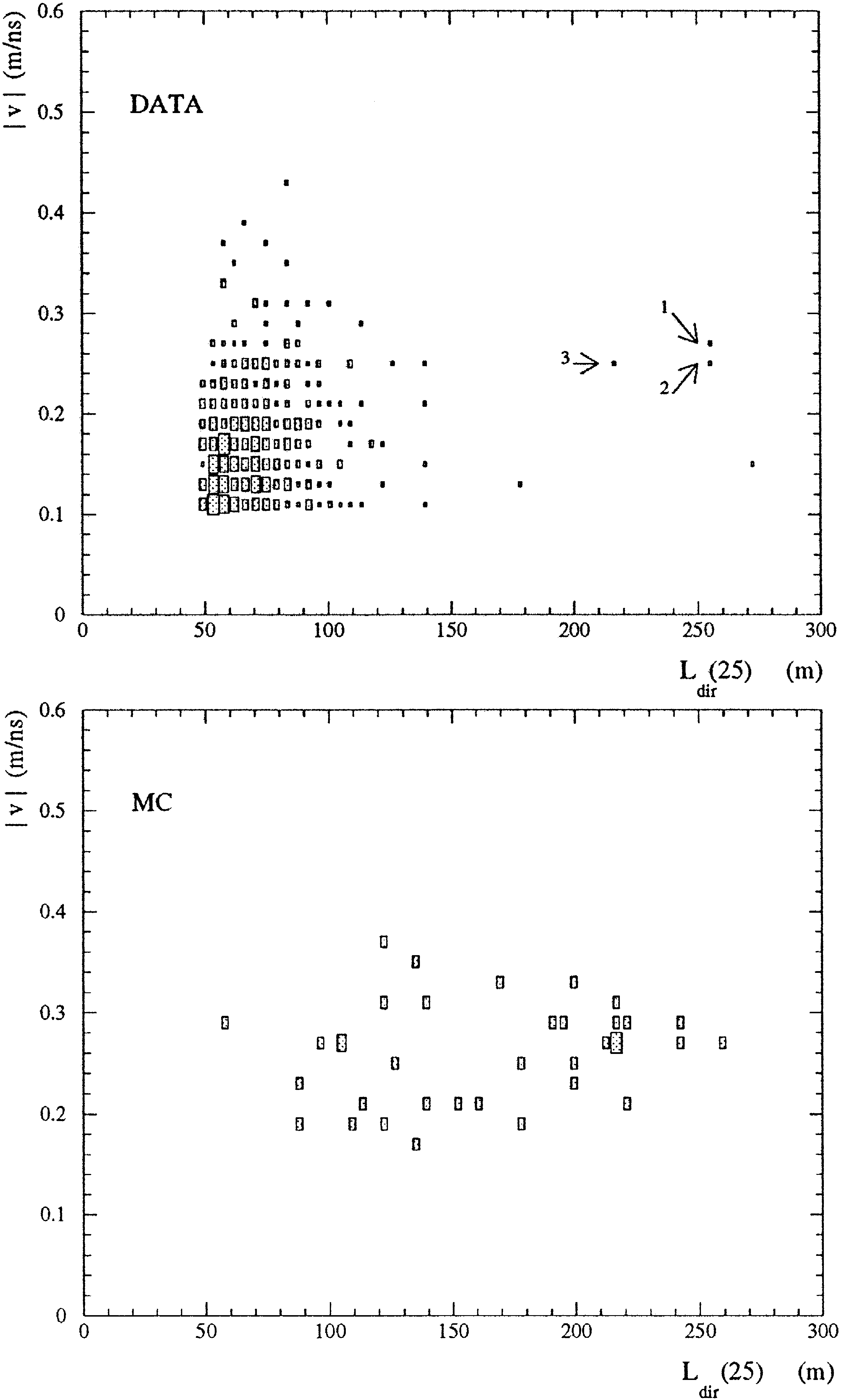
Fig. 22 shows the distribution when

and

25 are relaxed. The 3 events are marked by

dir

arrows. There is one additional event at high

25 ,

dir

which, however, has a somewhat too small

. The 3

events fall into the region populated by MC gener

ated atmospheric neutrino events passing the same

cuts bottom of Fig. 22 . We attribute the lack of

()

E. Andres et al.

Astroparticle Physics 13 2000 1–20

Table1

Characteristics of the events reconstructed as upgoing muons

Event ID

“

147742 4 706879 2 324428 8 427905

13 14 15 8

34 3 2

string

log

8.3

8.5

8.0

11.2

hit

, degrees 168.7 165.9 166.7 175.4

rec

, degrees 45.8 274.2 194.1 –

rec

experimental events between

;

150–200 to

dir

statistical fluctuations.

Due to CPU limitation we could not check the

agreement between experimental data and atmo

spheric muon MC down to a 8.9

reduction.

However, down to a reduction of 10

, the disagree

ment does not exceed a factor of 3. A less conserva

tive estimate of the accuracy of the signal prediction

can be obtained by replacing all dedicated cuts for

)

by the complementary cuts for

.We

observed a betterthan10% agreement between ex

perimental data and MC after all cuts. In conclusion

we estimate the uncertainty in the prediction of

upward muon neutrinos to be about a factor 2.

Table 1 summarizes the characteristics of the

neutrino candidates identified in the two analyses.

We conclude that tracks reconstructed as upgoing

are found at a rate consistent with that expected for

atmospheric neutrinos. The three events found in the

second analysis are well separated from background

proving that, even with a detector as small as

AMANDAB4, neutrino candidates can be separated

within a limited zenith angle interval. Meanwhile, a

few tens of clear neutrino events have been identi

fied with the more powerful AMANDAB10 tele

scope. They will be the subject of a forthcoming

paper.

10. Conclusions

We have described the design, operation, calibra

tion and selected results of the prototype neutrino

telescope AMANDAB4 at the South Pole.

The main results can be summarized as follows:

AMANDAB4 consisting of 80 optical modules

6 OMs for technology tests on 4 strings has

been deployed at depths between 1.5 and 2.0 km

in 1996. Seven of the OMs failed during refreez

ing. We have developed reliable drilling and in

strumentation procedures allowing deployment of

a 2 km deep string in less than a week. In the

mean time the detector has been upgraded to 302

. .

AMANDAB4, 1997 and 424 1998 optical

modules.

The ice properties between 1.5 and 2.0 km are

superior to those at shallow depths. The absorp

tion length is about 95 m and the effective scatter

ing length about 24 m.

The original calibration accuracy reached for ge

ometry and timing of AMANDAB4 was about 2

m and 7 nsec, respectively. With the upgrade to

10 strings, these values have been improved to

0.5–1.0 m and 5 nsec.

We have developed proper methods for track

reconstruction in a medium with nonnegligible

scattering. With tailored quality cuts, the remain

ing badly reconstructed tracks can be removed.

The quality of the reconstruction and the effi

ciency of the cuts improve considerably with

increasing size of the array.

Geometry and tracking accuracy of AMANDA

can be calibrated with surface air shower detec

tors. The mismatch between showers detected in

the SPASE air shower array and muons detected

with AMANDA is about 4 degrees, in agreement

with Monte Carlo estimates of the angular accu

racy.

The measured angular spectrum of the intensity

of atmospheric muons is in good agreement with

other experiments and with model calculations.

First neutrino candidates have been separated with

AMANDAB4. The identification of upward

muon candidates with an array of only 73 operat

ing 8inch PMTs is a demonstration that deep

antarctic ice is an adequate medium for doing

neutrino astronomy.

AMANDAB4 is a first step towards a large

neutrino telescope at the South Pole. A tenstring

array, AMANDAB10, has been taking data since

1997. Presently, B10 data are analyzed, and tens of

clear neutrino candidates have been extracted, with a

threshold of typically 50 GeV. The construction of

AMANDAII, a 30000 m

array, is underway. The

()

E. Andres et al.

Astroparticle Physics 13 2000 1–20

longterm goal of the collaboration is a cube kilome

ter detector, ICECUBE.

Acknowledgements

This research was supported by the U.S. National

Science Foundation, Office of Polar Programs and

Physics Division, the University of Wisconsin

Alumni Research Foundation, the U.S. Department

of Energy, the U.S. National Energy Research Scien

tific Computing Center, the Swedish Natural Science

Research Council, the Swedish Polar Research Sec

retariat, the Knut and Alice Wallenberg Foundation,

Sweden, and the Federal Ministery for Education and

Research, Germany. C.P.H. acknowledges the sup

port of the European Commission through TMR

contract No. ERBFMBICT91551.

We thank the Polar Ice Coring Office, PICO, for

bore hole drilling, and the Antarctic Support Associ

ates, ASA, as well as the staff of the Amundsen

Scott station for support and assistance. We grate

fully acknowledge help from the SPASE collabora

tion, Leeds University, and the U.K. Particle Physics

and Astrophysics Research Council.

References

1 T. Gaisser, F. Halzen, T. Stanev, Phys. Rep. 258 1995 174.

2 A. Bottino et al., Astropart. Phys. 2 1994 77.

3 L. Bergstrom, J. Edsjo, astroph

9607237.

¨¨

4 F. Halzen, J. Jacobsen, E. Zas, Phys. Rev. D 49 1994 1758.

5 J.L. Thorn et al., Phys. Rev. D 46 1992 4846.

6 Z. Djilkibaev, Proc. Int. Workshop on Simulation and Analy

sis Methods for Large Neutrino Telescopes, Zeuthen, Ger

many 1998 .

7 I.A. Belolaptikov et al., Astropart. Phys. 7 1997 263.

8 P. Askebjer et al., Science 267 1995 1147.

9 AMANDA Collaboration, J. Glaciology 41 1995 445.

10 Project Description Baikal 9203 DESY 1992 ; V. Balkanov

et al., astroph

9903342.

11 DUMAND II Proposal HDC288 Hawaii, 1988 .

12 S. Matsuno et al., Nucl. Instr. & Methods A 276 1989 359.

13 L.K. Resvanis et al., Proc. High Energy Neutrino Astro

physics Workshop, Hawaii, X. Tata, ed. World Scientific,

Singapore, 1992 p. 325.

14 ANTARES Proposal 1997; astroph

9707136.

15 D.M. Lowder et al., Nature 353 1991 331.

16 Yu.F. Barkov et al. Moscow Glaciological Research Publi

cation, 1984 .

17 R. Wischnewski et al., Proc. 24th Int. Cosmic Ray Conf.,

Rome, Italy 1 1995 p. 658.

18 R. Porrata et al., Proc. 25th Int. Cosmic Ray Conf., Durban,

South Africa 7 1997 237.

19 D. Lowder, K. Woschnagg, Proc. Int. Workshop on Simula

tion and Analysis Methods for Large Neutrino Telescopes,

Zeuthen, Germany 1998 .

20 S.N. Boziev et al., INR Preprint P0630 Moscow, Russia,

1989 .

21 E. Scapparone, Proc. Int. Workshop on Simulation and Anal

ysis Methods for Large Neutrino Telescopes, Zeuthen, Ger

many 1998 , and references therein.

22 L. Volkova, Sov. J. Nucl. Phys. 31 1980 784.

23 W. Lohmann, R. Kopp, R. Voss, CERN 8503 1985 .

24 S. Hundertmark, Proc. Int. Workshop on Simulation and

Analysis Methods for Large Neutrino Telescopes, Zeuthen,

Germany 1998 .

25 V.J. Stenger, University of Hawaii, HDC190; see also J.

Jacobsen, PhD thesis, http:

alizarin.physics.wisc.edu

jacobsen.

26 A. Bouchta, PhD thesis, Stockholm 1998, USIP Report 9807.

27 C. Wiebusch, Proc. Int. Workshop on Simulation and Analy

sis Methods for Large Neutrino Telescopes, Zeuthen, Ger

many 1998 .

28 D. Pandel, Diploma thesis HumboldtUniversity Berlin,

1996 .

29 C. Wiebusch et al., Proc. 25th Int. Cosmic Ray Conf.,

Durban, South Africa 7 1997 13.

30 A. Biron et al., Upgrade of AMANDAB towards

AMANDAII, DESY PRC 97

05, http:

www.ifh.de

amanda

publications

proposal.

31 J. Dickinson et al., Proc. 25th Int. Cosmic Ray Conf.,

Durban, South Africa 5 1997 233.

32 J. Dickinson et al., Proc. 25th Int. Cosmic Ray Conf.,

Durban, South Africa 5 1997 229.

33 T. Miller et al., Proc. 25th Int. Cosmic Ray Conf., Durban,

South Africa 5 1997 237.

34 J. Beaman et al., Phys. Rev. D 48 1993 4495.

35 T.K. Gaisser et al., Proc. 24th Int. Cosmic Ray Conf., Rome,

Italy 1 1995 938.

36 V. Blobel, Unfolding in High Energy Physics, DESY84118,

1984, and Regularized Unfolding for High Energy Physics

Experiments, Opal Note TN361 1996 .

37 G. Zech, Comparing Statistical Date to Monte Carlo Simula

tion: Parameter Fitting and Unfolding, DESY95113 June

1995 .

38 E. Bugaev et al., Phys. Rev. D 58 1998 .

39 C. Allkover, Cosmic Rays on Earth Karlsruhe, 1984 .

40 W. Rhode, PhD thesis, Wuppertal 1993 .

41 M. Crouch et al., Phys. Rev. D 18 1978 2239.

42 C. Berger et al., Phys. Rev. D 40 1989 2163.

43 M. Ambrosio et al., Phys. Rev. D 52 1995 3793.

44 P. Lipari, Astropart. Phys. 1 1993 1995.

45 J. Babson et al., Phys. Rev. D 42 1990 41.

46 T. Gaisser, Cosmic Rays and Particle Physics Cambridge

Univ. Press, Cambridge, 1990 .

47 E. Dahlberg, USIP Report 9802, Stockholm 1997.